Sempre me foi ensinado que em todas as ocasiões possíveis eu deveria simplificar as equações, não sendo apresentadas para mim restrições a isso.
No entanto, há alguns dias foi me apresentado uma equação em que, simplificando, havia perda de uma resposta da equação, como no caso:

No entanto, ao resolver um exercício hoje pela manhã, me deparei com:
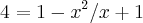 , onde a resolução se fazia por meio de simplificação.
, onde a resolução se fazia por meio de simplificação.Minha dúvida consiste em saber quando posso simplificar uma equação e quando não posso.
Obrigado.



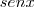 . Então a restrição aqui é de que
. Então a restrição aqui é de que  deve ser diferente de
deve ser diferente de 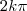 para
para 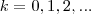 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

