 por odra1974 » Sáb Nov 19, 2011 13:44
por odra1974 » Sáb Nov 19, 2011 13:44
Bom dia
Estou tentando faz um dia e não consigo resolver a integral
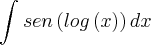
O problema é que ao desenvolver o cálculo chego a um ponto e fico bloqueado, pois não consigo terminar com a integral.
Cheguei até aqui e acho que não dá saida para eliminar a integral, pois parece que entra num ciclo vicioso
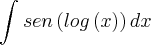
=
=
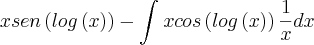
Me ajudem...
Abraços
-
odra1974
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Nov 19, 2011 13:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por LuizAquino » Sáb Nov 19, 2011 14:53
por LuizAquino » Sáb Nov 19, 2011 14:53
odra1974 escreveu:Estou tentando faz um dia e não consigo resolver a integral
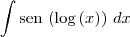
(...)
Cheguei até aqui e acho que não dá saida para eliminar a integral, pois parece que entra num ciclo vicioso
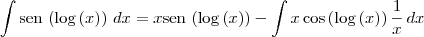
Você está usando a convenção de que

representa o logaritmo natural? Isto é, o logaritmo na base
e?
Se for isso, então de fato você pode usar que
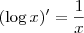
quando aplicar a integração por partes.
Mas se por outro lado você está usando a convenção de que

representa o logaritmo na base 10, então lembre-se que
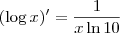
(onde aqui "ln" representa o logaritmo natural -- ou seja, na base
e).
Vou considerar que você está usando a convenção de que

representa
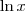
.
Para continuar a resolução, faça
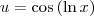
e

. Dessa forma, note que:
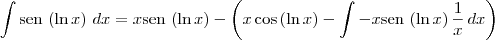
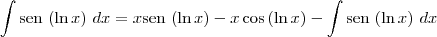
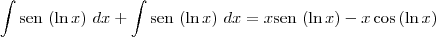
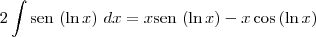
![\int \textrm{sen}\,\left(\ln x \right)\,dx = \frac{1}{2}\left[x \textrm{sen}\,\left(\ln x \right) - x\cos \left( \ln x \right)\right] + c \int \textrm{sen}\,\left(\ln x \right)\,dx = \frac{1}{2}\left[x \textrm{sen}\,\left(\ln x \right) - x\cos \left( \ln x \right)\right] + c](/latexrender/pictures/967e4650bdf1f6849f36a5758483c6d4.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por odra1974 » Sáb Nov 19, 2011 22:49
por odra1974 » Sáb Nov 19, 2011 22:49
Puxa! Muito obrigado! Essa passagem parece que foi mágica! Afinal, é tão simples...
-
odra1974
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Nov 19, 2011 13:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INTEGRAL DEFINIDA] logaritmo natural
por fabriel » Qua Jan 16, 2013 16:55
- 1 Respostas
- 1904 Exibições
- Última mensagem por Cleyson007

Qua Jan 16, 2013 17:24
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2577 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1856 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2746 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo (UF-CE)
por JailsonJr » Sáb Mai 22, 2010 04:56
- 6 Respostas
- 5283 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:32
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
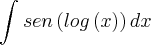
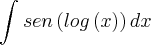 =
=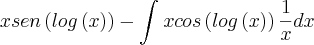


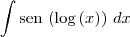
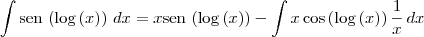
 representa o logaritmo natural? Isto é, o logaritmo na base
representa o logaritmo natural? Isto é, o logaritmo na base 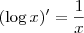 quando aplicar a integração por partes.
quando aplicar a integração por partes.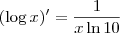 (onde aqui "ln" representa o logaritmo natural -- ou seja, na base
(onde aqui "ln" representa o logaritmo natural -- ou seja, na base 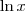 .
.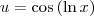 e
e  . Dessa forma, note que:
. Dessa forma, note que: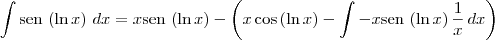
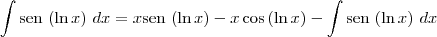
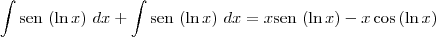
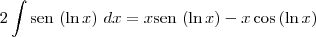
![\int \textrm{sen}\,\left(\ln x \right)\,dx = \frac{1}{2}\left[x \textrm{sen}\,\left(\ln x \right) - x\cos \left( \ln x \right)\right] + c \int \textrm{sen}\,\left(\ln x \right)\,dx = \frac{1}{2}\left[x \textrm{sen}\,\left(\ln x \right) - x\cos \left( \ln x \right)\right] + c](/latexrender/pictures/967e4650bdf1f6849f36a5758483c6d4.png)
