 por lyviston » Sáb Mar 07, 2009 01:41
por lyviston » Sáb Mar 07, 2009 01:41
Olá pessoal
estou tendo dificuldade em calcular as possibilidade de forma uma centena de acordo um conjuto de elementos
exemplo:
elementos 1,2,3,4
tentei assim
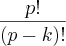
sendo p= numero de elementos = 4
k = 3
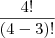
= 24
ate ai funcionou mais agora não da certo com os elementos 1,1,2,3 ou seja quando teve a repetição de um elemento ( 1 )
sei q o resultado teria q ser 12 gostaria de saber o caminho para se chegar a esse resultado sendo q tenho q fazer uma forma q ele aceite aumentar o numero de elementos e tbm de repetições
obrigado
-
lyviston
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mar 07, 2009 01:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por lyviston » Sáb Mar 07, 2009 13:03
por lyviston » Sáb Mar 07, 2009 13:03
ja tentei dividir o resultato pelo fatorial de repetições o q deu certo com 1,1,2,3 mas quando aumento o numero de elementos exemplo 1,1,2,3,4 não da certo
60/2! = 30 sendo q o certo seria 33
tbm vou ter q testar depois ele da seguinte forma 1,1,1,2,3 = 13 e 1,1,2,2,3 q da 18
obrigado
-
lyviston
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mar 07, 2009 01:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por Molina » Sáb Mar 07, 2009 13:42
por Molina » Sáb Mar 07, 2009 13:42
Boa Tarde, Lyviston.
Permutações com repetições podem ser escritas da seguinte forma:
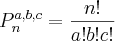
Onde
n é o número de elementos do conjunto e
a, b, c... são quantas vezes um certo elemento se repete dentro desse conjunto.
No caso de
1,1,2,3 há
4 elementos e o número 1 se repete
2 vezes, sendo assim
n=4 e
a=2, logo:
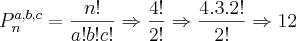
Faça os outros dessa forma que dará certo.
Bom estudo.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por lyviston » Sáb Mar 07, 2009 16:14
por lyviston » Sáb Mar 07, 2009 16:14
Boa tarde Diego
Seguindo essa logica tendo como elementos 1,1,2,2,3 da errado
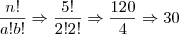
sendo que o certo seria 18
Obrigado.
-
lyviston
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mar 07, 2009 01:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por Molina » Seg Mar 09, 2009 23:32
por Molina » Seg Mar 09, 2009 23:32
Boa noite, Lyviston.
Você tem absoluta certeza que 18 é o resultado? Pergunto isso porque pelas duas fórmulas que existem para isso, o resultado dá 30. Ou estamos pensando em alguma coisa errada ou seu gabarito pode estar errado.
Sem utilizar a fórmula que já descrevi a cima, tem também outra maneira:
Com os elementos 1,1,2,2,3, temos:
*
dois 1
*
dois 2
*
um 3
Podemos descrever então:

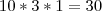
Coloque aqui suas idéias.
Abraços e bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Arranjo
por Pri Ferreira » Qua Mar 21, 2012 13:34
- 3 Respostas
- 2510 Exibições
- Última mensagem por LuizAquino

Seg Abr 09, 2012 23:30
Estatística
-
- Arranjo ! URGENTEEEEE
por my2009 » Qui Jun 03, 2010 19:08
- 3 Respostas
- 1615 Exibições
- Última mensagem por my2009

Sex Jun 04, 2010 23:07
Estatística
-
- Arranjo ou combinação?
por cristina » Sex Ago 27, 2010 11:41
- 3 Respostas
- 2325 Exibições
- Última mensagem por profmatematica

Sáb Ago 28, 2010 05:08
Estatística
-
- Arranjo ou Combinação?
por gustavowelp » Sex Nov 19, 2010 07:22
- 2 Respostas
- 1406 Exibições
- Última mensagem por gustavowelp

Sex Nov 19, 2010 13:36
Estatística
-
- Probabilidade de um arranjo
por ihavenokia » Qua Out 26, 2011 15:12
- 2 Respostas
- 2048 Exibições
- Última mensagem por jose henrique

Qua Out 26, 2011 21:05
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
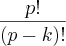
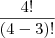 = 24
= 24

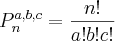
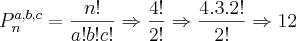


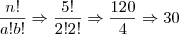

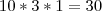
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
