


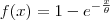 é necessário usar a Regra da Cadeia. Ficaremos com:
é necessário usar a Regra da Cadeia. Ficaremos com: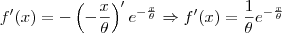
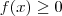 para todo x no domínio e
para todo x no domínio e 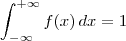 .
.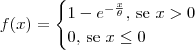
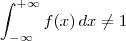 .
.
LuizAquino escreveu:Para derivar a funçãoé necessário usar a Regra da Cadeia. Ficaremos com:
Se f(x) é a função densidade de probabilidade da variável aleatória contínua X, devemos terpara todo x no domínio e
.
Considere agora a função:
Apesar dessa função ser maior ou igual a zero para todo x no seu domínio, note que.
Nesse contexto, f não pode ser uma função densidade de probabilidade. Não fará sentido você querer calcular E[X].
Qual é o texto completo do exercício?
Além disso, aproveito para informar que você não deve postar o texto do exercício como uma imagem, pois isso prejudica as ferramentas de busca. Por favor, sempre digite o texto do exercício.

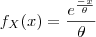 . Então
. Então 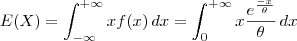 . Agora é resolver por partes.
. Agora é resolver por partes.

MarceloFantini escreveu:Derivando, temos que. Então
. Agora é resolver por partes.


MarceloFantini escreveu:Sim, integração por partes.



MarceloFantini escreveu:Tente resolver sem os limites para encontrar a primitiva, e depois aplique os limites no resultado.

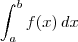 , que tem uma primitiva. O que você vai fazer é resolver a integral indefinida
, que tem uma primitiva. O que você vai fazer é resolver a integral indefinida 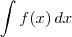 , encontrar a primitiva
, encontrar a primitiva  e retornar à integral original, fazendo
e retornar à integral original, fazendo 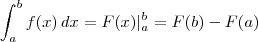 .
.

MarceloFantini escreveu:Com aplicar os limites que quero dizer o seguinte: você tem a integral definida, que tem uma primitiva. O que você vai fazer é resolver a integral indefinida
, encontrar a primitiva
e retornar à integral original, fazendo
.

Inference escreveu:Essa função que você derivou não é uma função densidade e sim um função de distribuição.
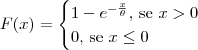 , com
, com  .
.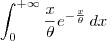
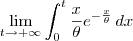
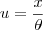 e
e 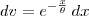 , portanto
, portanto 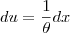 e
e 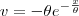 ). Após resolver a integral, você fica com algo como F(t) - F(0) (com F primitiva de f). Daí, basta resolver o limite:
). Após resolver a integral, você fica com algo como F(t) - F(0) (com F primitiva de f). Daí, basta resolver o limite: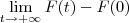

LuizAquino escreveu:Inference escreveu:Essa função que você derivou não é uma função densidade e sim um função de distribuição.
Vamos esclarecer as definições. Para essa função do exercício ser uma função de distribuição acumulada, estamos considerando:, com
.
Agora você deseja calcular a integral imprópria:
Para fazer isso, você deve resolver o limite:
Como o colega Fantini falou, essa integral é resolvida por partes (por exemplo, fazendoe
, portanto
e
). Após resolver a integral, você fica com algo como F(t) - F(0) (com F primitiva de f). Daí, basta resolver o limite:
Observação
É recomendado que você revise o conteúdo de integrais impróprias.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: