 por Inference » Qua Ago 03, 2011 13:03
por Inference » Qua Ago 03, 2011 13:03
Amigos, vocês poderiam me ajudar a derivar essa função em relação a x?
Depois disso como eu integro a E(X)? Ou seja, preciso integrar de 0 a infinito, o resultado a derivação inicial vezes x.
Obrigado!
- Anexos
-

- questão.jpg (11.45 KiB) Exibido 4162 vezes
-
Inference
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 03, 2011 12:44
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qui Ago 04, 2011 21:37
por LuizAquino » Qui Ago 04, 2011 21:37
Para derivar a função
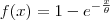
é necessário usar a
Regra da Cadeia. Ficaremos com:
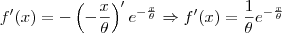
Se f(x) é a
função densidade de probabilidade da variável aleatória contínua X, devemos ter
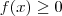
para todo x no domínio e
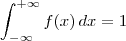
.
Considere agora a função:
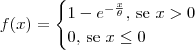
Apesar dessa função ser maior ou igual a zero para todo x no seu domínio, note que
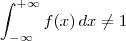
.
Nesse contexto, f não pode ser uma função densidade de probabilidade. Não fará sentido você querer calcular E[X].
Qual é o texto completo do exercício?
Além disso, aproveito para informar que você não deve postar o texto do exercício como uma imagem, pois isso prejudica as ferramentas de busca. Por favor, sempre digite o texto do exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Inference » Sex Ago 05, 2011 11:48
por Inference » Sex Ago 05, 2011 11:48
LuizAquino escreveu:Para derivar a função
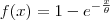
é necessário usar a
Regra da Cadeia. Ficaremos com:
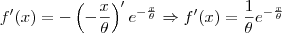
Se f(x) é a
função densidade de probabilidade da variável aleatória contínua X, devemos ter
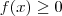
para todo x no domínio e
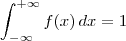
.
Considere agora a função:
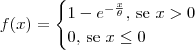
Apesar dessa função ser maior ou igual a zero para todo x no seu domínio, note que
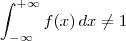
.
Nesse contexto, f não pode ser uma função densidade de probabilidade. Não fará sentido você querer calcular E[X].
Qual é o texto completo do exercício?
Além disso, aproveito para informar que você não deve postar o texto do exercício como uma imagem, pois isso prejudica as ferramentas de busca. Por favor, sempre digite o texto do exercício.
Luiz, primeiramente obrigado pela sua resposta. Fico devendo o enunciado porque estou sem ele agora.
Essa função que você derivou não é uma função densidade e sim um função de distribuição. Você derivando a função de distribuição chega à função de densidade, que é essa que você achou pela Regra da Cadeia.
Agora que é a etapa que eu não estou conseguindo, que é achar a média dessa função f'(x) (integrando de 0 a infinito).
Obrigado!
-
Inference
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 03, 2011 12:44
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Sex Ago 05, 2011 13:35
por MarceloFantini » Sex Ago 05, 2011 13:35
Derivando, temos que
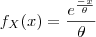
. Então
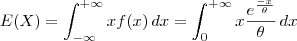
. Agora é resolver por partes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Inference » Sex Ago 05, 2011 13:45
por Inference » Sex Ago 05, 2011 13:45
MarceloFantini escreveu:Derivando, temos que
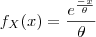
. Então
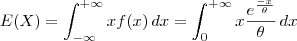
. Agora é resolver por partes.
Obrigado Marcelo! Exatamente! Como eu resolvo essa integral? Fazendo Integração por Partes?
Obrigado!
-
Inference
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 03, 2011 12:44
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Sex Ago 05, 2011 13:47
por MarceloFantini » Sex Ago 05, 2011 13:47
Sim, integração por partes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Inference » Sex Ago 05, 2011 14:19
por Inference » Sex Ago 05, 2011 14:19
MarceloFantini escreveu:Sim, integração por partes.
Estou com dificuldades de fazer essa integração, pois na expressão da integração por partes temos a expressão: INT (f(x) * g'(x))dx = f(x)*g(x) -
INT f'(x) * g(x) dxNão consigo resolver a expressão
INT f'(x) * g(x) dx (lembrando que ela tende também de 0 a infinito).
Eu lembro que há uma solução direta de integral de 0 a infinito para distribuição exponencial, mas acho que ela não se aplica nesse caso.
-
Inference
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 03, 2011 12:44
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Sex Ago 05, 2011 14:37
por MarceloFantini » Sex Ago 05, 2011 14:37
Tente resolver sem os limites para encontrar a primitiva, e depois aplique os limites no resultado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Inference » Sex Ago 05, 2011 14:50
por Inference » Sex Ago 05, 2011 14:50
MarceloFantini escreveu:Tente resolver sem os limites para encontrar a primitiva, e depois aplique os limites no resultado.
Eu posso resolver a integral sem o 0 e o infinito e depois aplico limites? Eu não sabia que posso resolver integrais tirando essa variação e depois aplico limites. Tentarei resolver desse jeito.
Muito obrigado!
-
Inference
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 03, 2011 12:44
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Sex Ago 05, 2011 14:58
por MarceloFantini » Sex Ago 05, 2011 14:58
Com aplicar os limites que quero dizer o seguinte: você tem a integral definida
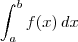
, que tem uma primitiva. O que você vai fazer é resolver a integral
indefinida 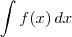
, encontrar a primitiva

e retornar à integral original, fazendo
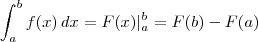
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Inference » Sex Ago 05, 2011 15:17
por Inference » Sex Ago 05, 2011 15:17
MarceloFantini escreveu:Com aplicar os limites que quero dizer o seguinte: você tem a integral definida
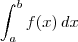
, que tem uma primitiva. O que você vai fazer é resolver a integral
indefinida 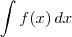
, encontrar a primitiva

e retornar à integral original, fazendo
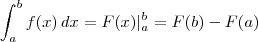
.
Ah tá, ok! Tinha entendido errado. Levei até um susto, rs...
Entendi, mas tenho que aplicar o infinito em F(x) = F(b) - F(a). Essa parte que não sei se consiguirei resolver. Irei fazer.
Obrigado!
-
Inference
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 03, 2011 12:44
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sex Ago 05, 2011 15:52
por LuizAquino » Sex Ago 05, 2011 15:52
Inference escreveu:Essa função que você derivou não é uma função densidade e sim um função de distribuição.
Vamos esclarecer as definições. Para essa função do exercício ser uma
função de distribuição acumulada, estamos considerando:
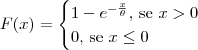
, com

.
Agora você deseja calcular a
integral imprópria:
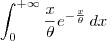
Para fazer isso, você deve resolver o limite:
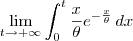
Como o colega Fantini falou, essa integral é resolvida por partes (por exemplo, fazendo
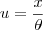
e
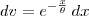
, portanto
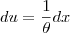
e
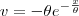
). Após resolver a integral, você fica com algo como F(t) - F(0) (com F primitiva de f). Daí, basta resolver o limite:
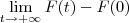 Observação
ObservaçãoÉ recomendado que você revise o conteúdo de integrais impróprias.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Inference » Sex Ago 05, 2011 17:05
por Inference » Sex Ago 05, 2011 17:05
LuizAquino escreveu:Inference escreveu:Essa função que você derivou não é uma função densidade e sim um função de distribuição.
Vamos esclarecer as definições. Para essa função do exercício ser uma
função de distribuição acumulada, estamos considerando:
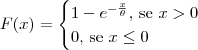
, com

.
Agora você deseja calcular a
integral imprópria:
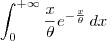
Para fazer isso, você deve resolver o limite:
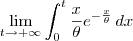
Como o colega Fantini falou, essa integral é resolvida por partes (por exemplo, fazendo
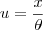
e
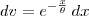
, portanto
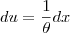
e
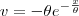
). Após resolver a integral, você fica com algo como F(t) - F(0) (com F primitiva de f). Daí, basta resolver o limite:
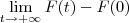 Observação
ObservaçãoÉ recomendado que você revise o conteúdo de integrais impróprias.
Ok Luiz e Fantini, muito obrigado pela ajuda!
Abs
Maurício (Inference)
-
Inference
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Ago 03, 2011 12:44
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em integração por partes !!!
por gerson25 » Qua Fev 23, 2011 23:01
- 2 Respostas
- 2713 Exibições
- Última mensagem por gerson25

Qui Fev 24, 2011 17:51
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL INDEFINIDA] Duvida de integração
por fabriel » Qua Out 03, 2012 16:20
- 3 Respostas
- 2093 Exibições
- Última mensagem por fabriel

Qua Out 03, 2012 17:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Duvida na integração Por partes
por fabriel » Sáb Out 06, 2012 18:56
- 1 Respostas
- 1589 Exibições
- Última mensagem por MarceloFantini

Sáb Out 06, 2012 19:17
Cálculo: Limites, Derivadas e Integrais
-
- [integração por partes] Dúvida teórica
por natanaelskt » Qui Jul 17, 2014 03:00
- 1 Respostas
- 1573 Exibições
- Última mensagem por e8group

Qui Jul 17, 2014 10:03
Cálculo: Limites, Derivadas e Integrais
-
- [Integração Definida] dúvida em integral com u.du
por Nicolas1Lane » Sáb Ago 30, 2014 20:36
- 3 Respostas
- 3399 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 21:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



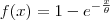 é necessário usar a Regra da Cadeia. Ficaremos com:
é necessário usar a Regra da Cadeia. Ficaremos com: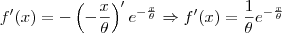
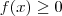 para todo x no domínio e
para todo x no domínio e 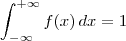 .
.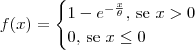
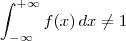 .
.
é necessário usar a Regra da Cadeia. Ficaremos com:
para todo x no domínio e
.
.

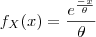 . Então
. Então 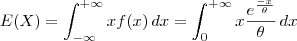 . Agora é resolver por partes.
. Agora é resolver por partes.

. Então
. Agora é resolver por partes.






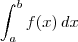 , que tem uma primitiva. O que você vai fazer é resolver a integral indefinida
, que tem uma primitiva. O que você vai fazer é resolver a integral indefinida 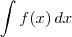 , encontrar a primitiva
, encontrar a primitiva  e retornar à integral original, fazendo
e retornar à integral original, fazendo 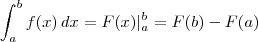 .
.

, que tem uma primitiva. O que você vai fazer é resolver a integral indefinida
, encontrar a primitiva
e retornar à integral original, fazendo
.

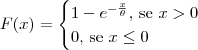 , com
, com  .
.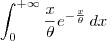
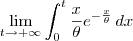
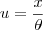 e
e 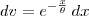 , portanto
, portanto 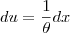 e
e 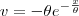 ). Após resolver a integral, você fica com algo como F(t) - F(0) (com F primitiva de f). Daí, basta resolver o limite:
). Após resolver a integral, você fica com algo como F(t) - F(0) (com F primitiva de f). Daí, basta resolver o limite: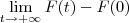

, com
.
e
, portanto
e
). Após resolver a integral, você fica com algo como F(t) - F(0) (com F primitiva de f). Daí, basta resolver o limite:
