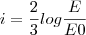 ,em que E é a energia instatanea liberada pelo terremoto,cuja a duração foi de 8segundos,variou em função do tempo conforme a equação
,em que E é a energia instatanea liberada pelo terremoto,cuja a duração foi de 8segundos,variou em função do tempo conforme a equação 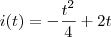 ,t em segundos e i em kwh,no instante em que a intensidade do terremoto era maxima,a energia liberada,em kwh,era de
,t em segundos e i em kwh,no instante em que a intensidade do terremoto era maxima,a energia liberada,em kwh,era dea-)
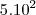
b-)
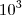
c-)
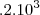
d-)
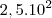
e-)
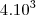




 .
.
 :
: