 por lorena Kelly » Sáb Dez 01, 2012 20:41
por lorena Kelly » Sáb Dez 01, 2012 20:41
Uma lata cilíndrica é feita para receber 1 litro de óleo. Encontre as dimensões
que maximizam o custo do metal para produzir a lata.
Dica:
Quanto menos metal, menos custo.
Procure utilizar área.
Faça o desenho para representar
h r A
h r V
cilindro ? ?
?
2 2
2
2
+ =
=
)
-
lorena Kelly
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Dez 01, 2012 20:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por lorena Kelly » Sáb Dez 01, 2012 20:45
por lorena Kelly » Sáb Dez 01, 2012 20:45
Me ajuda PROFESSORES, não sei fazer este exercicio.
-
lorena Kelly
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Dez 01, 2012 20:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Sáb Dez 01, 2012 21:28
por e8group » Sáb Dez 01, 2012 21:28
Dica, Tenta obter uma relação com os seguintes dados :
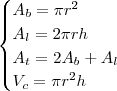
Onde :
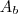
(Área base)
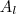
(Área Lateral)
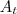
(Área total )
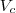
(Volume do cilindro)
Além das observações proposta pelo seu professor ,observe que a capacidade máxima do volume do cilindro é compativel com um litro de óleo .Em outras palavras ,

Tente concluir ,se não conseguir post algo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Sáb Dez 01, 2012 21:56
por Cleyson007 » Sáb Dez 01, 2012 21:56
Boa noite Lorena!
Seja bem-vinda ao Ajuda Matemática!
Santhiago, pensei da seguinte forma:
Seja
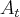
a área total,

o raio,
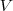
o volume, e

a altura.
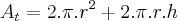
e
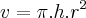
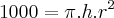
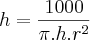
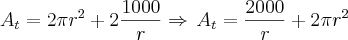
Derivando em relação a

, temos:
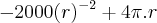
Derivada da área total -->
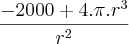
No ponto mínimo temos a derivada acima igual a zero. Logo:
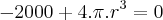
![r=\sqrt[3]{\frac{10}{2\pi}} r=\sqrt[3]{\frac{10}{2\pi}}](/latexrender/pictures/62e53c373bc35d9e7164a94ce3331903.png)
Para a altura, temos:
![h=\left( \frac{1000}{\pi.\frac{10}{\sqrt[3]{2\pi}}}\right)^{2} h=\left( \frac{1000}{\pi.\frac{10}{\sqrt[3]{2\pi}}}\right)^{2}](/latexrender/pictures/0b4a973315c2786fb2920c13ea95c7f1.png)
![h=\frac{20}{\sqrt[3]{2.\pi}} h=\frac{20}{\sqrt[3]{2.\pi}}](/latexrender/pictures/921a7b63bacc1b8d4cfba5b21236dc00.png)
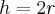
Bom, espero que esteja certo.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por e8group » Dom Dez 02, 2012 20:21
por e8group » Dom Dez 02, 2012 20:21
Boa noite , Cleyson007. No meu ponto de vista sua solução estar correta .Porém você mencionou que o volume é igual a
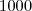
,isto seria
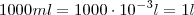
certo ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Ter Dez 04, 2012 10:34
por Cleyson007 » Ter Dez 04, 2012 10:34
Certo Santhiago.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10896 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13201 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14807 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5117 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


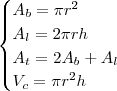
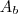 (Área base)
(Área base) 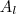 (Área Lateral)
(Área Lateral) 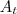 (Área total )
(Área total ) 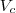 (Volume do cilindro)
(Volume do cilindro)

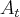 a área total,
a área total,  o raio,
o raio, 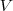 o volume, e
o volume, e  a altura.
a altura.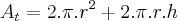 e
e 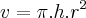
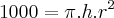
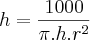
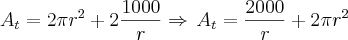
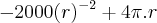
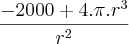
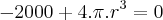
![r=\sqrt[3]{\frac{10}{2\pi}} r=\sqrt[3]{\frac{10}{2\pi}}](/latexrender/pictures/62e53c373bc35d9e7164a94ce3331903.png)
![h=\left( \frac{1000}{\pi.\frac{10}{\sqrt[3]{2\pi}}}\right)^{2} h=\left( \frac{1000}{\pi.\frac{10}{\sqrt[3]{2\pi}}}\right)^{2}](/latexrender/pictures/0b4a973315c2786fb2920c13ea95c7f1.png)
![h=\frac{20}{\sqrt[3]{2.\pi}} h=\frac{20}{\sqrt[3]{2.\pi}}](/latexrender/pictures/921a7b63bacc1b8d4cfba5b21236dc00.png)
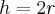

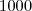 ,isto seria
,isto seria 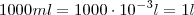 certo ?
certo ?

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.