Geometria de Novo

por **Ansso** » Qui Out 21, 2010 22:31

As retas de equações r1: y+2x-4 = 0, r2: 3y+4x-12 = 0 e r3: y+x-4 = 0 determinam com os eixos coordenados regiões triangulares, respectivamente, R1, R2 e R3, contidas no 1º quadrante do plano xOy. Girando-se R1, R2 e R3, 360°em torno do eixo Oy, obtêm-se sólidos S1, S2 e S3, cujos volumes V1, V2 e V3
A) são iguais.
B) formam uma progressão aritmética.
C) formam uma progressão geométrica.
D) são tais que V1 = 4V2 - 2V3.
E) são tais que V1/2 = V2/3 = V3/4

Gabarito - D

Só uma pergunta as coordenadas fica pra: r1(2, 4), r2(3, 4) e r3(4, 4). Está correto? Depois não consigo vizualizar os sólidos girando como ele pede. E gostaria de saber um livro de Matemática completo bom. O vestibular que quero fazer não é nada mole.

Obrigado pela Atenção. Vcs são fera! :y:

por **MarceloFantini** » Qui Out 21, 2010 23:58

Eu estou imaginando um cone para cada um deles, pena que é difícil desenhar. Qual vestibular você vai prestar? Pense que o raio é da origem até onde cada reta corta o eixo x.

por **Ansso** » Sex Out 22, 2010 12:58

Vou fazer Eng. da Computação na Uefs(BA). Pelo desenho que eu fiz com essas coordenadas só conseguir um retângulo. Não sei aonde entraria o raio nessa questão.!

por **MarceloFantini** » Sex Out 22, 2010 14:29

Então você fez o desenho errado, uma reta não faz um retângulo no primeiro quadrante. Desenhe as retas e tente visualizar a rotação.

por **cassiele** » Sex Out 22, 2010 15:13

01.SE O PONTO (a,b) É O CENTRO DA CIRCUNFERENCIA DE AQUAÇÃO X2+Y2+3X-4Y+2=0 ,O PONTO (a,-b) PERTENCE AO:

a)PRIMEIRO QUADRANTE
b)SEGUNDO QUADRANTE
c)TECEIRO QUADRANTE
d)EIXO DAS ABSCISSAS
e)EIXO DAS ORDENADAS

ja tentei de tudo , fiz assim o achei o centro da equaçao que e -3/2 e 2 mas so ate ai mais nada me ajudem por favor e raiz e tembem ja consegui

por **MarceloFantini** » Sex Out 22, 2010 15:29

Cassiele, crie um novo tópico pra sua dúvida.

por **cassiele** » Sex Out 22, 2010 15:37

por **cassiele** » Sex Out 22, 2010 15:40

responda estou a 4 dias tentando responder essas questoes e nada me ajude por favor

por **DanielRJ** » Sex Out 22, 2010 15:45

edite sua msg para evitar double post. e outra só descer a barra de rolagem da pagina inicial na secção "duvidas de Matematica" e clica na materia que deseja postar.

por **Ansso** » Ter Out 26, 2010 10:12

Fantini, tentei fazer a questão como vc disse pelas retas mas não saiu a resposta! Tem como responder ela sem fazer o desenho? Pesquisei nos livros de Mat aqui nas férias e não achei nenhuma se quer parecida. Essa pergunta da pra responder por aqui mesmo?

por **MarceloFantini** » Ter Out 26, 2010 12:51

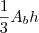As retas cortam o eixo x nos pontos 2, 3 e 4, respectivamente. Desenhando você verá três triângulos, todos cortando o eixo y no ponto 4. Os sólidos gerados por rotação em torno do eixo OY são cones, cujos raios são as distãncias da origem até onde cortam o eixo x e as alturas são as distãncias da origem até onde cortam o eixo y, no caso, todas iguais. O volume de um cone é $\frac{1}{3}A_b h$ . O volume do cone 1 é 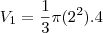$V_1 = \frac{1}{3}\pi(2^2).4$ , volume do cone 2 é 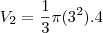$V_2 = \frac{1}{3}\pi(3^2).4$ e o volume do cone 3 é 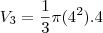$V_3 = \frac{1}{3}\pi(4^2).4$ . Claramente, não formam uma P.G. e nem uma P.A., e também não são iguais. Sobram duas alternativas. Testando a E, você vê que é falsa, só sobra a D.