 por natanskt » Sex Out 15, 2010 19:08
por natanskt » Sex Out 15, 2010 19:08
1-)(EEAR)se
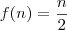
se n é par e
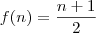
,se n é impar,define uma função
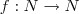
,ENTÃO
a-)f é apenas injetora
b-)f é bijetora
c-)f não é injetora,nem sobrejetora
d-)f é apenas sobrejetora
não consiguir fazer
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por MarceloFantini » Sex Out 15, 2010 20:30
por MarceloFantini » Sex Out 15, 2010 20:30
Natanskt, você sabe os significados de injetora, sobrejetora e bijetora?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielRJ » Sex Out 15, 2010 22:01
por DanielRJ » Sex Out 15, 2010 22:01
Se par:
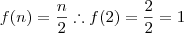
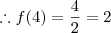
Se ímpar:
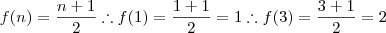
Bom não ficou muito boa mais da pra entender.Vamos lá:
Ela é
sobrejetora quando todos os elementos de B estão relacionados.
Ela é
injetora quando elementos de B estão relacionados uma vvez só.
Ela é
Bijetora quando for sobrejetora e injetora ao mesmo tempo.
Bom é isso ai só uma previa da materia, mas você tem que estudar com um prof° antes de começar a materia. na AFA não cai questoes desse tipo. agora já da pra responder.Obs: O anexo foi em baixo pois n sei coloca-lo no meioGabarito letra (D)
- Anexos
-
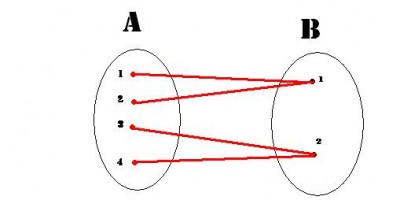
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por natanskt » Sex Out 15, 2010 22:11
por natanskt » Sex Out 15, 2010 22:11
eu sei,o problema é que não consigo intender o que pede,e nem como faz
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por natanskt » Sex Out 15, 2010 22:12
por natanskt » Sex Out 15, 2010 22:12
valeu daniel,o minha dificuldade era fazer a conta
brigadão
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por natanskt » Sex Out 15, 2010 22:13
por natanskt » Sex Out 15, 2010 22:13
eu não sabia que podia chutar o valor
ahsuhusa
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (EEAR)Função
por natanskt » Sex Out 15, 2010 19:18
- 4 Respostas
- 6099 Exibições
- Última mensagem por Elcioschin

Sáb Out 16, 2010 19:13
Funções
-
- (EEAR)Função
por natanskt » Ter Out 19, 2010 10:40
- 1 Respostas
- 2475 Exibições
- Última mensagem por DanielRJ

Ter Out 19, 2010 16:37
Funções
-
- (EEAR)Função
por natanskt » Qua Out 20, 2010 12:04
- 1 Respostas
- 2128 Exibições
- Última mensagem por DanielRJ

Qua Out 20, 2010 12:25
Funções
-
- (EEAR)Função 2 grau
por natanskt » Sex Out 22, 2010 11:54
- 3 Respostas
- 2012 Exibições
- Última mensagem por DanielFerreira

Sex Nov 19, 2010 19:14
Funções
-
- (EEAR)Função 2 grau
por natanskt » Sex Out 22, 2010 13:57
- 1 Respostas
- 1108 Exibições
- Última mensagem por MarceloFantini

Sex Out 22, 2010 14:34
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
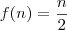 se n é par e
se n é par e 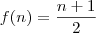 ,se n é impar,define uma função
,se n é impar,define uma função 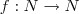 ,ENTÃO
,ENTÃO
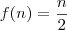 se n é par e
se n é par e 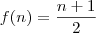 ,se n é impar,define uma função
,se n é impar,define uma função 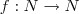 ,ENTÃO
,ENTÃO


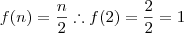
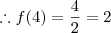
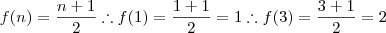






![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)