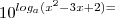
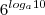 ,está no conjunto:
,está no conjunto:a-){1,2,3,4}
b-){-4,-3,-2,-1,0,1}
c-){-1,0,1,2,3,4}
d-){0,1,2,3,4}
pimeiramente corte os
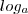 deixei apenas os logaritimando,pode fazer isso?
deixei apenas os logaritimando,pode fazer isso?não consigo fazer,me ajuda
abraços

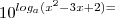
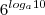 ,está no conjunto:
,está no conjunto: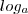 deixei apenas os logaritimando,pode fazer isso?
deixei apenas os logaritimando,pode fazer isso?
natanskt escreveu:11-)sendo a>0 e a diferente de 1,o conjunto solução da equação,está no conjunto:
a-){1,2,3,4}
b-){-4,-3,-2,-1,0,1}
c-){-1,0,1,2,3,4}
d-){0,1,2,3,4}
pimeiramente corte osdeixei apenas os logaritimando,pode fazer isso?
não consigo fazer,me ajuda
abraços
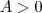 e
e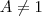 (logico porque é a bse é claro!) eu não sei se estou correto ,mas podemos escolher valores para A.e nesse caso eu escolhendo a=10 fica evidente uma propriedade de logaritmos no primeiro membro, que Fala quando as bases forrem iguais o resultado será o logaritmando. ok? então vamos lá.
(logico porque é a bse é claro!) eu não sei se estou correto ,mas podemos escolher valores para A.e nesse caso eu escolhendo a=10 fica evidente uma propriedade de logaritmos no primeiro membro, que Fala quando as bases forrem iguais o resultado será o logaritmando. ok? então vamos lá.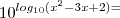
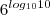
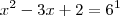
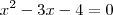


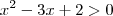
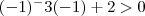
 --->Ok!
--->Ok!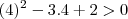
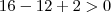
 ---->Ok!
---->Ok!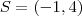




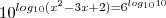
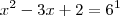

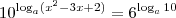
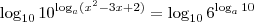
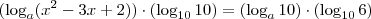
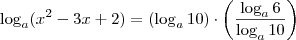
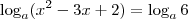


natanskt escreveu:
não intendi essa passagem, 6^1 eu intendi mais e o 10 do outro lado???
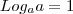 sempre!
sempre!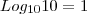
Fantini escreveu:Solução incorreta do ponto de vista formal. Você escolheu um caso particular de base, e essa resolução não funciona pra outros casos. Vou fazer a resolução mais geral:
Tomando o logaritmo decimal dos dois lados:
Como as bases são iguais, podemos igualar os logaritmandos e resolver verificando as condições, mas a partir daí você pode ver pelo post do Daniel. É importante que você veja o método geral porque a maneira como o Daniel resolveu não pode ser usada pra qualquer outra.



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)