 por DanielRJ » Qui Out 07, 2010 17:20
por DanielRJ » Qui Out 07, 2010 17:20
Bom pessoal para não ficar criando topicos seguidos vou postar duas questão neste ,pois a acho que será rapido, ok?1 - A solução da equação

a)

b)
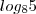
c)

d)
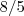
e)0
Bom inicialmente passei o

pro outro lado e transformei a equação em um log veja:

Isso procede?
Vamos pra segunda questão:
2 - O menor valor de n para o qual se tem

a)2
b)3
c)4
d)10
e)100
A dificuldade nesta questão é resolver esta parte que não entendo.Bom é isso eu tenho mais algumas duvidas mas posso sanar-lás no deecorrer das respostas
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Out 07, 2010 18:01
por MarceloFantini » Qui Out 07, 2010 18:01

Como

, então só sobra

Segunda: note que

e

. Então:

O menor valor
inteiro de n tal que

é 4.
Faltou o problema dizer que
n é inteiro.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielRJ » Sex Out 08, 2010 14:40
por DanielRJ » Sex Out 08, 2010 14:40
Bom fantini vamos por partess..
1 questão:
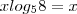

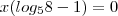
colocou em evidencia? não teria outra maneira de ser feito isso?
e logaritmos sempre darão um resultado diferente de zero né?
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Sex Out 08, 2010 18:08
por Elcioschin » Sex Out 08, 2010 18:08
danielcdd
1) Sim, colocou em evidência
2) Não existe outro meio não: colocando em evidência obtém-s uma forma fatorada. Um dos fatores deve ser igual a zero.
3) log55 = 1 ----> Logo, log58 > 1 ----> log58 - 1 > 0
4) Como o fator (log58 - 1) é diferente de zero -----> O outro fator é x = 0
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por DanielRJ » Sáb Out 09, 2010 15:28
por DanielRJ » Sáb Out 09, 2010 15:28
Obrigado ai pela explicação amigoo..foi muito bem expicdado.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:27
- 2 Respostas
- 1881 Exibições
- Última mensagem por Molina

Sex Out 08, 2010 14:30
Funções
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:30
- 1 Respostas
- 1466 Exibições
- Última mensagem por DanielRJ

Sex Out 08, 2010 14:13
Funções
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 13:31
- 1 Respostas
- 1682 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 13:42
Logaritmos
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 14:51
- 2 Respostas
- 1831 Exibições
- Última mensagem por natanskt

Seg Out 11, 2010 15:58
Logaritmos
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 15:00
- 1 Respostas
- 1646 Exibições
- Última mensagem por Douglasm

Sáb Out 09, 2010 17:29
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


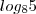

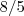
 pro outro lado e transformei a equação em um log veja:
pro outro lado e transformei a equação em um log veja: Isso procede?
Isso procede?



 , então só sobra
, então só sobra 
 e
e  . Então:
. Então:
 é 4.
é 4.

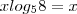

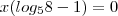 colocou em evidencia? não teria outra maneira de ser feito isso?
colocou em evidencia? não teria outra maneira de ser feito isso?