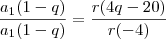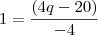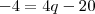Boa tarde.
Por definição, podemos escrever o 1°, 5° e 21° termos da PA da seguinte forma, respectivamente:

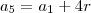
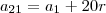
E como esses termos formam uma PG, e sabemos que se eu pegar um termo da PG e dividir pelo termo anterior, nos fornece a razão, temos as seguintes equações:
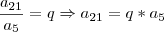
e
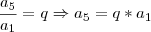
Substituindo esses valores e ajustando ela melhor, você chegará em:

e
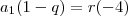
Dividindo a de cima pela de baixo:
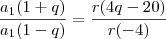
Note aqui que o
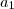
e o

irão se anular. Multiplicando cruzado cairemos numa equação do 2° grau:
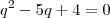
onde as raízes são 4 e 1. Como se a razão de uma PG for 1 ela é constante, ficamos com

.
Não fiz uma prova real para ve se esse é o valor correto. Então, caso você faça, poste aqui!
Bom estudo!




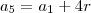
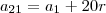
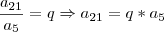
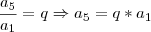

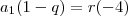
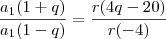
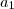 e o
e o  irão se anular. Multiplicando cruzado cairemos numa equação do 2° grau:
irão se anular. Multiplicando cruzado cairemos numa equação do 2° grau: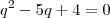
 .
.

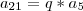
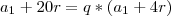
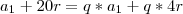


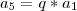 em
em