 então o termo dessa PA é?
então o termo dessa PA é?Comecei a resolver assim:
S=(a1+an)/2
 =(a1+an)/2
=(a1+an)/2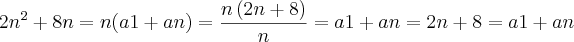
eu consegui resolver até, mas não sei se esta maneira de resolver está correta e a partir daí começou a ficar obscuro a solução para mim, quem puder me ajudar agradeço.

 então o termo dessa PA é?
então o termo dessa PA é? =(a1+an)/2
=(a1+an)/2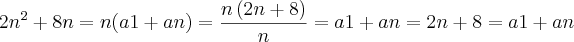

jose henrique escreveu:A soma dos n primeiros termos de uma pa éentão o termo dessa PA é?
Comecei a resolver assim:
S=(a1+an)/2=(a1+an)/2
eu consegui resolver até, mas não sei se esta maneira de resolver está correta e a partir daí começou a ficar obscuro a solução para mim, quem puder me ajudar agradeço.
 já é a formula que ele te dá para voce achar os termos então basta substituir:
já é a formula que ele te dá para voce achar os termos então basta substituir: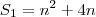
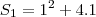
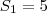

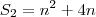
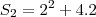

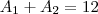 então vamos descobrir
então vamos descobrir 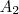 e a razão tambem
e a razão tambem 
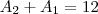
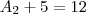
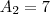
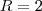



jose henrique escreveu:Obrigado desde já pela ajuda, mas eu esqueci de colocar que ele está pedindo o termo geral e que o meu gabarito do meu livro está constando 2n+3

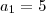




Fantini escreveu:Não há nada de errado. Veja:
Você só não montou o termo geral, mas a resolução do daniel te deu o primeiro termo e a razão.

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)