 por jose henrique » Sáb Set 25, 2010 10:02
por jose henrique » Sáb Set 25, 2010 10:02
A soma dos n primeiros termos de uma pa é

então o termo dessa PA é?
Comecei a resolver assim:
S=(a1+an)/2

=(a1+an)/2
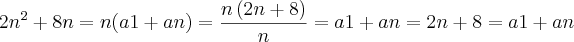
eu consegui resolver até, mas não sei se esta maneira de resolver está correta e a partir daí começou a ficar obscuro a solução para mim, quem puder me ajudar agradeço.
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por jose henrique » Sáb Set 25, 2010 22:38
por jose henrique » Sáb Set 25, 2010 22:38
Obrigado desde já pela ajuda, mas eu esqueci de colocar que ele está pedindo o termo geral e que o meu gabarito do meu livro está constando 2n+3
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por DanielRJ » Sáb Set 25, 2010 23:12
por DanielRJ » Sáb Set 25, 2010 23:12
jose henrique escreveu:Obrigado desde já pela ajuda, mas eu esqueci de colocar que ele está pedindo o termo geral e que o meu gabarito do meu livro está constando 2n+3
Bom então vamos esperar um professor pra responder talvez cometi algum equivoco.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielRJ » Dom Set 26, 2010 15:39
por DanielRJ » Dom Set 26, 2010 15:39
Fantini escreveu:Não há nada de errado. Veja:
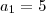


Você só não montou o termo geral, mas a resolução do daniel te deu o primeiro termo e a razão.
Ah.. bom ele queria o termo geral..vlw
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 então o termo dessa PA é?
então o termo dessa PA é? =(a1+an)/2
=(a1+an)/2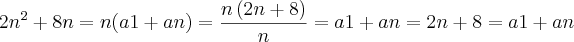

 então o termo dessa PA é?
então o termo dessa PA é? =(a1+an)/2
=(a1+an)/2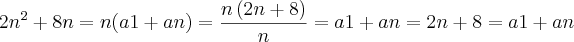

então o termo dessa PA é?
=(a1+an)/2
 já é a formula que ele te dá para voce achar os termos então basta substituir:
já é a formula que ele te dá para voce achar os termos então basta substituir: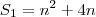
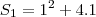
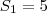

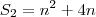
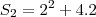

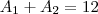 então vamos descobrir
então vamos descobrir 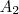 e a razão tambem
e a razão tambem 
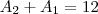
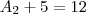
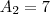
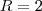




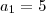







 , avisa que eu resolvo.
, avisa que eu resolvo.

