 por hmspriss » Qui Set 23, 2010 11:13
por hmspriss » Qui Set 23, 2010 11:13
o exercício pede para calcular o volume de
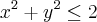
e
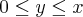
o resultado era para ser
![4\pi(\sqrt[]{2}-1)/3 4\pi(\sqrt[]{2}-1)/3](/latexrender/pictures/a422565e1e628fcc695d547c34df99b4.png)
fiz os calculo usando a fórmula v=
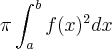
mas o resultado deu
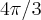
, acho que o problema está no intervalo da integração, eu coloquei de 0 até 1, qual seria o intervalo correto?
-
hmspriss
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Set 23, 2010 10:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por MarceloFantini » Sex Set 24, 2010 01:32
por MarceloFantini » Sex Set 24, 2010 01:32
O raio da semi-circunferência é
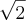
, e não 1. Logo:


Talvez eu tenha esquecido alguma coisa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integrais] Volume de um sólido obtido por rotação
 por Leon » Sex Dez 05, 2014 16:05
por Leon » Sex Dez 05, 2014 16:05
- 1 Respostas
- 3584 Exibições
- Última mensagem por Leon

Sex Dez 05, 2014 16:52
Cálculo: Limites, Derivadas e Integrais
-
- Volume de Sólido pela Rotação em torno do Eixo y.
por diegodiscovery » Dom Jun 13, 2010 16:27
- 0 Respostas
- 3344 Exibições
- Última mensagem por diegodiscovery

Dom Jun 13, 2010 16:27
Cálculo: Limites, Derivadas e Integrais
-
- [Volume de um sólido obtido pela rotação em torno do eixo X]
por EmiliaMat » Ter Mai 06, 2014 21:16
- 1 Respostas
- 5454 Exibições
- Última mensagem por brunaraujo

Seg Jun 24, 2019 11:00
Cálculo: Limites, Derivadas e Integrais
-
- volume do sólido obtido pela rotação em torno de uma reta
por Fernandobertolaccini » Sáb Jul 26, 2014 19:31
- 0 Respostas
- 2170 Exibições
- Última mensagem por Fernandobertolaccini

Sáb Jul 26, 2014 19:31
Cálculo: Limites, Derivadas e Integrais
-
- Integrais - Volume por Rotação
por elisafrombrazil » Dom Abr 16, 2017 11:17
- 0 Respostas
- 4820 Exibições
- Última mensagem por elisafrombrazil

Dom Abr 16, 2017 11:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
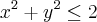 e
e 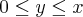 o resultado era para ser
o resultado era para ser ![4\pi(\sqrt[]{2}-1)/3 4\pi(\sqrt[]{2}-1)/3](/latexrender/pictures/a422565e1e628fcc695d547c34df99b4.png)
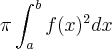 mas o resultado deu
mas o resultado deu 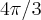 , acho que o problema está no intervalo da integração, eu coloquei de 0 até 1, qual seria o intervalo correto?
, acho que o problema está no intervalo da integração, eu coloquei de 0 até 1, qual seria o intervalo correto?
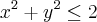 e
e 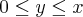 o resultado era para ser
o resultado era para ser ![4\pi(\sqrt[]{2}-1)/3 4\pi(\sqrt[]{2}-1)/3](/latexrender/pictures/a422565e1e628fcc695d547c34df99b4.png)
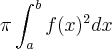 mas o resultado deu
mas o resultado deu 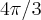 , acho que o problema está no intervalo da integração, eu coloquei de 0 até 1, qual seria o intervalo correto?
, acho que o problema está no intervalo da integração, eu coloquei de 0 até 1, qual seria o intervalo correto?
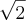 , e não 1. Logo:
, e não 1. Logo:



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.