Olá, estou com dúvidas na resolução das matrizes inversas
por exemplo:
2a+ 4c 2b+ad 1 0
a+5c b+5d = 0 1
pela igualdade de matrizes consegui achar o A (eu acho..) :
2a + 4c= 1
a + 5c= 0
fiz:
2a + 4c= 1 x5
a + 5c= 0 x4
10a + 20c = 5
-4a - 20c = 0
6a = 5
a= 5/6 o resultado confere , mas quando tento achar o 'C' não ñ bate com a resposta certa que é: -1/6
Me ajudem tenho que aprender matriz inversa até terça!
obrigada


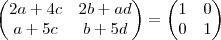



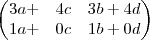
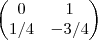
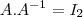 A original multiplicado pela inversa sempre é a Matriz identidade.
A original multiplicado pela inversa sempre é a Matriz identidade.
 .
.
 :
: