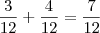A probabilidade de escolher um número ímpar depende de qual número passou do conjunto A para o conjunto B, certo? Então vamos analisar as duas possibilidades (do elemento passado ser par OU do elemento passado ser ímpar).
1) Elemento é par.
Existem 2 elementos pares em A num total de 4 elementos:

. _
Assim, o novo grupo B apresenta 3 nºs ímpares de 6 elementos:
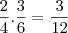
, essa é a probabilidade de se retirar um nº ímpar de B caso o elemento inserido de A seja par. Mas, vamos analisar a probabilidade caso o elemento de A seja ímpar:
2) Elemento é ímpar.
Existem 2 elementos ímpares num total de 4.

. _
Assim, o novo grupo B apresenta 4 nºs ímpares num total de 6 números.
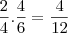
: Probababilidade de retirar um nº ímpar de B caso o elemento retirado de A seja ímpar.
Concluindo: O elemento de A pode ser par ou ímpar: então vamos somar as duas probabilidades:
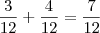
Letra D.
Qq coisa, pode falar. Se tiver algum erro tbm.
=**
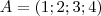 e
e 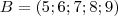 . Passa-se ao acaso um elemento do conjunto
. Passa-se ao acaso um elemento do conjunto  para o conjunto
para o conjunto  e depois escolhe-se, tambem ao acaso, um elemento de
e depois escolhe-se, tambem ao acaso, um elemento de  . A probabilidade deste elemento ser ímpar é:
. A probabilidade deste elemento ser ímpar é:


 . _
. _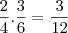 , essa é a probabilidade de se retirar um nº ímpar de B caso o elemento inserido de A seja par. Mas, vamos analisar a probabilidade caso o elemento de A seja ímpar:
, essa é a probabilidade de se retirar um nº ímpar de B caso o elemento inserido de A seja par. Mas, vamos analisar a probabilidade caso o elemento de A seja ímpar: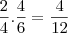 : Probababilidade de retirar um nº ímpar de B caso o elemento retirado de A seja ímpar.
: Probababilidade de retirar um nº ímpar de B caso o elemento retirado de A seja ímpar.