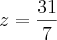por my2009 » Qui Set 16, 2010 11:54
por my2009 » Qui Set 16, 2010 11:54
Bom dia. Eu já tentei resolver esse sistema várias vezes e por mais que seja simples sempre dá errado.
 x+ 5y - z = -5
x+ 5y - z = -5
y + 2z =6
x-3z= -11Obrigada !
Obs : Ao resolver, por favor faça pelo método tradicional. Não faça por matriz.
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielRJ » Qui Set 16, 2010 12:35
por DanielRJ » Qui Set 16, 2010 12:35
Olá amiga eu fiz pelo metodo de escalonamento e deu certinho.
z=3 , y=0 e x=-2
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por my2009 » Qui Set 16, 2010 12:48
por my2009 » Qui Set 16, 2010 12:48
Olá daniel cdd , obrigada pq vc colocou as respostas =) , mas se eu postei aqui é pq não entendi o processo... ¬¬
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por my2009 » Qui Set 16, 2010 12:58
por my2009 » Qui Set 16, 2010 12:58
Agora eu mesma consegui fazer XD , Obrigada ! Hj eu estou mais tranquila então consegui entender melhor e resolver
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielRJ » Qui Set 16, 2010 13:57
por DanielRJ » Qui Set 16, 2010 13:57
Desculpa é que hj to meio preguiçoso mas já que voce achou a resposta não precisa posta xD.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por filipepaixao » Qua Set 29, 2010 10:46
por filipepaixao » Qua Set 29, 2010 10:46
Eu tentei resolver da forma como está em anexo (Método de Eliminação de Gauss) mas onde estou eu a errar???
visto que
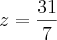
Abraço
- Anexos
-
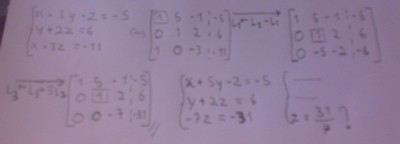
-

filipepaixao
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Set 29, 2010 09:48
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Programação de Sistemas
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3093 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema linear] Sistema linear com constante
por smlspirit » Qui Jul 19, 2012 19:34
- 4 Respostas
- 5568 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 22:40
Sistemas de Equações
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4501 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema linear
por kael » Ter Out 20, 2009 14:14
- 1 Respostas
- 2676 Exibições
- Última mensagem por kael

Ter Out 20, 2009 16:24
Sistemas de Equações
-
- Sistema Linear
por kael » Qua Out 21, 2009 13:43
- 1 Respostas
- 3642 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2009 15:26
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.