 por Balanar » Dom Ago 29, 2010 03:57
por Balanar » Dom Ago 29, 2010 03:57
Os pontos P e Q pertencem ao interior do segmento AB e estão de um mesmo lado do seu ponto médio. P divide AB na razão 2/3 e Q divide AB na razão 3/4 . Se PQ=2cm, calcule AB.
Resposta:
70 cm
To tendo dificuldade de montar o segmento, o exercício está na parte que envolve razão da secção interna e externa.
Por favor detalhe principalmente como você monto o segmento,caso tenha conseguido fazer.
Grato desde já.
To tendo dificuldades para cocnseguir montar o segmento correto, o mais difícil e montar o segmento de forma correta (to tentando fazer isso)
Eu tentei o segunite...
A.......................P............Q...............M.............B
Minha interpretação ta sendo essa mas não ta dando gabarito.
Se poderem ajudar grato desde já.
Abraços
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Dom Ago 29, 2010 15:55
por Douglasm » Dom Ago 29, 2010 15:55
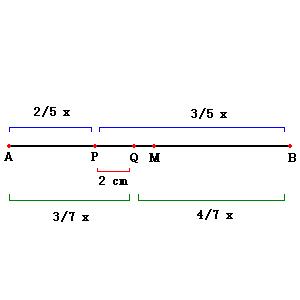
- segmento.JPG (6.94 KiB) Exibido 8319 vezes
Acho que o desenho que fiz já é bastante elucidativo, mas acompanhe:
- Chamaremos o comprimento de
AB de
"x";
- Se
P divide o segmento
AB na proporção
2/3, logo
P divide o segmento
AB em dois segmentos menores,
2/5 x e
3/5 x.
- Analogamente,
Q divide o segmento
AB em dois segmentos medindo
3/7 x e
4/7 x, respectivamente.
Como podemos observar no desenho:
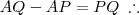


-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Balanar » Dom Ago 29, 2010 17:15
por Balanar » Dom Ago 29, 2010 17:15
Muito bom a resposta vlw.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Balanar » Dom Ago 29, 2010 18:33
por Balanar » Dom Ago 29, 2010 18:33
Como você essa figura? Você uso algum programa?
Como eu poderia fazer uma figura semelhante a essa?
Aguardo resposta.
Grato desde já.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Dom Ago 29, 2010 19:14
por Douglasm » Dom Ago 29, 2010 19:14
Bom, eu só usei o Paint. xD
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação da Reta] Bissetriz interna e externa
por Marcos_Mecatronica » Sex Mai 17, 2013 21:48
- 1 Respostas
- 2971 Exibições
- Última mensagem por Marcos_Mecatronica

Ter Mai 21, 2013 21:09
Geometria Analítica
-
- Bissetriz Interna e Bissetriz Externa
por sauloandrade » Seg Nov 05, 2012 18:13
- 0 Respostas
- 2087 Exibições
- Última mensagem por sauloandrade

Seg Nov 05, 2012 18:13
Geometria Analítica
-
- Circunferência inscrita numa secção circular
 por Guga1981 » Ter Out 17, 2017 19:14
por Guga1981 » Ter Out 17, 2017 19:14
- 1 Respostas
- 3314 Exibições
- Última mensagem por Guga1981

Ter Out 17, 2017 19:16
Geometria Plana
-
- (GEOMETRIA PLANA) Area total externa - Planificação Sólid
 por gusavancini » Qui Ago 18, 2016 12:16
por gusavancini » Qui Ago 18, 2016 12:16
- 0 Respostas
- 4089 Exibições
- Última mensagem por gusavancini

Qui Ago 18, 2016 12:16
Geometria Plana
-
- [Triângulo retângulo] Bissetriz interna
por Ricardo MB » Seg Jul 21, 2014 22:44
- 0 Respostas
- 2062 Exibições
- Última mensagem por Ricardo MB

Seg Jul 21, 2014 22:44
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


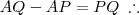



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
