 por lidimedeiros » Dom Ago 29, 2010 12:28
por lidimedeiros » Dom Ago 29, 2010 12:28
Gente me ajudem por favor nesse problema da faculdade!
No seu primeiro ano de existencia, o lucro de uma empresa foi de R$32.000,00. Seus dois sócios, Cléber e Ricardo, dividiram o lucro de forma diretamente proporcional ao tempo de cada um na sociedade, já que Ricardo iniciou suas atividades na empresa 8 meses depois de Cléber. Quanto coube a cada um, sendo que o capital investido por ambos foi o mesmo.
a)R$16.000,00 a ambos
b)R$18.000,00 e R$14.000,00
c)R$24.000,00 e R$8.000,00
d)R$23.000,00 e R$9.000,00
e)R$20.000,00 e R$12.000,00
Preciso do passo a passo pois é discursiva.
-
lidimedeiros
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Ago 29, 2010 12:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por DanielRJ » Seg Ago 30, 2010 00:17
por DanielRJ » Seg Ago 30, 2010 00:17
vamos chamar socio A de Cleber e socio B de Ricardo:
lucro da empresa = 32 mil logo

Dizer que é diretamente proporcional significa divisão então:
ms primeiro iremos calcular o tempo de cada um na empresa.
no primeiro ano de existencia Cleber já estava na empresa então ele tem 1 ano. já ricardo entrou 8 meses depois então ele terá 4 meses.
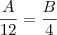
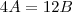
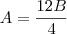
subistiuindo..
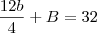
igualando as bases.
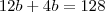
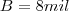
achando A.
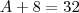
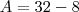
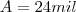
cara questão fácil se voce tivesse quebrado a cabeça um poukinho acharia a resposta.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisão de lucros - URGENTE
por torrel » Qui Mai 06, 2010 10:26
- 0 Respostas
- 681 Exibições
- Última mensagem por torrel

Qui Mai 06, 2010 10:26
Matemática Financeira
-
- Descontos e Lucros
por karinaforlin » Sáb Abr 03, 2010 22:58
- 0 Respostas
- 2614 Exibições
- Última mensagem por karinaforlin

Sáb Abr 03, 2010 22:58
Matemática Financeira
-
- Divisão por Zero
por harumitu » Qui Mar 29, 2012 07:07
- 1 Respostas
- 3408 Exibições
- Última mensagem por MarceloFantini

Qui Mar 29, 2012 10:47
Álgebra Elementar
-
- Divisão
por alvessp » Qui Ago 21, 2014 04:17
- 1 Respostas
- 2578 Exibições
- Última mensagem por Russman

Sex Ago 22, 2014 22:16
Cálculo: Limites, Derivadas e Integrais
-
- Divisão
por antonybel » Seg Dez 09, 2019 17:32
- 1 Respostas
- 6202 Exibições
- Última mensagem por adauto martins

Qui Dez 12, 2019 13:47
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



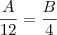
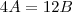
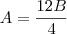 subistiuindo..
subistiuindo..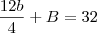 igualando as bases.
igualando as bases.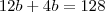
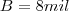 achando A.
achando A.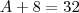
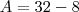
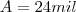

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.