 por jose henrique » Sex Ago 13, 2010 18:57
por jose henrique » Sex Ago 13, 2010 18:57
Determine a relação entre a e b onde a e b são números naturais que expressan os números de alagarismos de x=
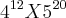
e Y=
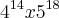
x=
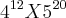
=
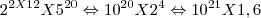
Y=
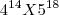
=
![{2}^{2X14}X{5}^{18}\Leftrightarrow[tex]{2}^{2X14}X{5}^{18}\Leftrightarrow{2}^{28}X{5}^{18}\Leftrightarrow{10}^{18}X{2}^{10} {2}^{2X14}X{5}^{18}\Leftrightarrow[tex]{2}^{2X14}X{5}^{18}\Leftrightarrow{2}^{28}X{5}^{18}\Leftrightarrow{10}^{18}X{2}^{10}](/latexrender/pictures/6e4bc68044aed634dae561247060478d.png)
a relação dada no gabarito é a=b, porém não consegui chegar a está conclusão
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por alexandre32100 » Sáb Ago 14, 2010 14:00
por alexandre32100 » Sáb Ago 14, 2010 14:00
Está certo até o ponto em que você parou.
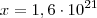
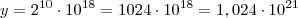
Podemos ver que tanto

, quanto

tem
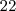
dígitos. Ou seja,
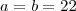
.
-
alexandre32100
-
 por jose henrique » Sáb Ago 14, 2010 16:44
por jose henrique » Sáb Ago 14, 2010 16:44
Obrigado pela explicação, porém qual a regra para chegar a quantidade de dígitos, pois muitas vezes me deparo com exercícios que pedem para determinar a quantidade de dígitos
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por alexandre32100 » Sáb Ago 14, 2010 17:45
por alexandre32100 » Sáb Ago 14, 2010 17:45
Não é bem uma regra. Mas por exemplo
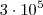
é

seguido de
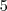
zeros, logo tem

dígitos.
A exemplo do exercício,
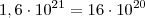
equivale a
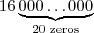
, ou seja, tem
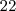
dígitos.
O mesmo raciocínio pode ser usado para o
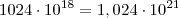
.

Mas, se quiser transformar isso em uma regra, pode-se dizer que:
"O número 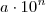 , com
, com 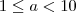 e
e 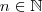 , tem
, tem  dígitos."
dígitos."
-
alexandre32100
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3690 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3779 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
-
- [Potencia] soma de potencia com letras
por carla villela » Qui Mar 01, 2012 21:04
- 8 Respostas
- 8638 Exibições
- Última mensagem por carla villela

Qui Mar 01, 2012 22:18
Sistemas de Equações
-
- Potenciação - Potência de potência
por Ana Paula MMS » Sáb Jan 11, 2014 14:59
- 1 Respostas
- 2641 Exibições
- Última mensagem por Cleyson007

Sáb Jan 11, 2014 17:27
Aritmética
-
- (Potencia) equação com potencia
por Thiago1986Iz » Dom Jul 24, 2016 12:53
- 1 Respostas
- 2046 Exibições
- Última mensagem por DanielFerreira

Dom Jul 24, 2016 16:00
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
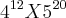 e Y=
e Y=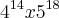
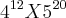 =
=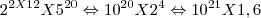
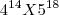 =
=![{2}^{2X14}X{5}^{18}\Leftrightarrow[tex]{2}^{2X14}X{5}^{18}\Leftrightarrow{2}^{28}X{5}^{18}\Leftrightarrow{10}^{18}X{2}^{10} {2}^{2X14}X{5}^{18}\Leftrightarrow[tex]{2}^{2X14}X{5}^{18}\Leftrightarrow{2}^{28}X{5}^{18}\Leftrightarrow{10}^{18}X{2}^{10}](/latexrender/pictures/6e4bc68044aed634dae561247060478d.png)

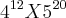 e Y=
e Y=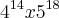
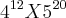 =
=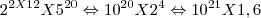
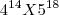 =
=![{2}^{2X14}X{5}^{18}\Leftrightarrow[tex]{2}^{2X14}X{5}^{18}\Leftrightarrow{2}^{28}X{5}^{18}\Leftrightarrow{10}^{18}X{2}^{10} {2}^{2X14}X{5}^{18}\Leftrightarrow[tex]{2}^{2X14}X{5}^{18}\Leftrightarrow{2}^{28}X{5}^{18}\Leftrightarrow{10}^{18}X{2}^{10}](/latexrender/pictures/6e4bc68044aed634dae561247060478d.png)

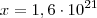
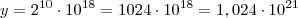
 , quanto
, quanto  tem
tem 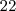 dígitos. Ou seja,
dígitos. Ou seja, 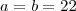 .
.
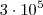 é
é  seguido de
seguido de 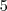 zeros, logo tem
zeros, logo tem  dígitos.
dígitos.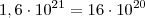 equivale a
equivale a 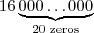 , ou seja, tem
, ou seja, tem 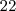 dígitos.
dígitos.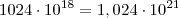 .
. 
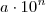 , com
, com 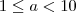 e
e 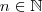 , tem
, tem  dígitos."
dígitos."

 , avisa que eu resolvo.
, avisa que eu resolvo.

