 por rsholtermann » Qua Jul 14, 2010 13:21
por rsholtermann » Qua Jul 14, 2010 13:21
(Vunesp)
Dado um quadrado plano ABCD, escolhem-se 3 pontos sobre o lado AB, 5 pontos sobre o lado BC, 2 pontos sobre CD e 1 ponto sobre AD, de tal modo que nenhum desses pontos coincida com algum vertice do quadrado. Seja X o conjunto dos pontos escolhidos. O numero de triangulos com vertices em X é: (R:154)
primeiro calculei a combinaçao de 11 elementos tomado 3 a 3 C11,3 = 11! / 3!8! e achei 165
so que eu nao sei como eu faço para eliminar as opçoes em que sao levado em conta os pontos colineares como no lado AB e o lado BC, que possuem 3 e 5 pontos, respectivamente. Por estarem alinhados nao formam triangulo, mas como eu retiro-os da conta ?? Obrigado
-
rsholtermann
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jul 14, 2010 13:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Jul 14, 2010 14:50
por MarceloFantini » Qua Jul 14, 2010 14:50
O conjunto dos pontos pode ser pensado como todas as combinações (
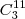
) menos as colineares (

). Logo:
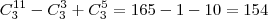
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Combinação de Numeros]Combinação até chegar em outro
por moacirrf » Dom Set 30, 2012 15:51
- 0 Respostas
- 1789 Exibições
- Última mensagem por moacirrf

Dom Set 30, 2012 15:51
Análise Combinatória
-
- Pontos Não-Colineares
 por wilgaroto » Sex Out 28, 2011 09:41
por wilgaroto » Sex Out 28, 2011 09:41
- 1 Respostas
- 4468 Exibições
- Última mensagem por LuizAquino

Sáb Out 29, 2011 11:51
Geometria Analítica
-
- Pontos Colineares
por Claudin » Qui Abr 05, 2012 19:19
- 3 Respostas
- 10687 Exibições
- Última mensagem por Claudin

Qui Abr 05, 2012 22:31
Geometria Analítica
-
- Pontos P,Q e R - Colineares ?
por PeterHiggs » Seg Set 24, 2012 19:10
- 2 Respostas
- 2467 Exibições
- Última mensagem por PeterHiggs

Ter Set 25, 2012 13:18
Geometria Espacial
-
- Pontos colineares
por Milton21 » Qui Out 18, 2012 15:14
- 4 Respostas
- 15825 Exibições
- Última mensagem por e8group

Sex Out 19, 2012 17:48
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


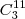 ) menos as colineares (
) menos as colineares ( ). Logo:
). Logo: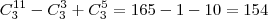



 .
.
 :
: