 por Jonatan » Qua Jul 07, 2010 21:57
por Jonatan » Qua Jul 07, 2010 21:57
Em uma cidade com n + 1 habitantes, n
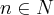
, uma pessoa passa uma nota de R$10,00 a uma segunda pessoa como troco de uma compra, esta segunda pessoa por sua vez passa esta mesma nota a uma terceira pessoa e assim sucessivamente. Determine a probabilidade de esta nota ser passada m vezes, m
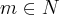
,

, sem retornar a primeira pessoa.
Gabarito:
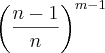
Pessoal, não faço nem ideia de como faz essa questão. Alguém pode resolver e explicar para mim? Obrigado desde já.
-
Jonatan
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Jun 16, 2010 13:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Douglasm » Qua Jul 07, 2010 23:54
por Douglasm » Qua Jul 07, 2010 23:54
Bom, é simples, veja só:
O primeiro a passar a nota, passa esta para um dos n habitantes restantes, que por sua vez, passa a nota para um dos (n-1) habitantes restantes. Como a única condição é que a nota não volte a PRIMEIRA pessoa, o terceiro indivíduo pode passar a nota para (n-1) habitantes (ele não pode passar para o primeiro, nem para si mesmo), assim como todos os outros depois dele. Como são feitas m passagens, o número de casos favoráveis que nós temos é:

Se excluírmos a condição inicial, cada um dos habitantes poderá passar a nota para os outros n habitantes restantes. Sendo assim, o número de casos totais é:
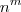
Como a probabilidade é definida como o número de casos favoráveis sobre o número de casos possíveis, ela é:
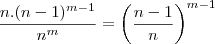
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade] Exercício Desafio de Probabilidade
por werwer » Qua Mar 21, 2012 18:57
- 0 Respostas
- 10348 Exibições
- Última mensagem por werwer

Qua Mar 21, 2012 18:57
Estatística
-
- [Dúvida]Um desafio que envolve probabilidade
por Gabi Biel » Qui Out 17, 2013 20:37
- 5 Respostas
- 3836 Exibições
- Última mensagem por temujin

Sáb Out 19, 2013 21:05
Probabilidade
-
- [DESAFIO DE PROBABILIDADE 2] Energia de uma feixe
por PTuga » Sáb Out 26, 2013 18:16
- 0 Respostas
- 1415 Exibições
- Última mensagem por PTuga

Sáb Out 26, 2013 18:16
Probabilidade
-
- [DESAFIO DE PROBABILIDADE] Tempo de espera na urgência
por PTuga » Sáb Out 26, 2013 18:11
- 0 Respostas
- 1244 Exibições
- Última mensagem por PTuga

Sáb Out 26, 2013 18:11
Probabilidade
-
- Desafio
por Guarinense » Sex Nov 10, 2017 22:25
- 0 Respostas
- 5654 Exibições
- Última mensagem por Guarinense

Sex Nov 10, 2017 22:25
Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
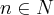 , uma pessoa passa uma nota de R$10,00 a uma segunda pessoa como troco de uma compra, esta segunda pessoa por sua vez passa esta mesma nota a uma terceira pessoa e assim sucessivamente. Determine a probabilidade de esta nota ser passada m vezes, m
, uma pessoa passa uma nota de R$10,00 a uma segunda pessoa como troco de uma compra, esta segunda pessoa por sua vez passa esta mesma nota a uma terceira pessoa e assim sucessivamente. Determine a probabilidade de esta nota ser passada m vezes, m 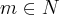 ,
,  , sem retornar a primeira pessoa.
, sem retornar a primeira pessoa.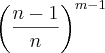



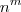
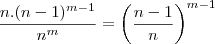



 , avisa que eu resolvo.
, avisa que eu resolvo.

