 por Carolziiinhaaah » Qua Jun 23, 2010 18:15
por Carolziiinhaaah » Qua Jun 23, 2010 18:15
Sejam as matrizes reais de ordem 2,
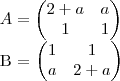
então, a soma dos elementos da diagonal principal de
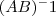
é igual a:
gabarito:
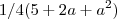
Então, eu achei oq está dentro do parênteses como resposta.. não entendi o porquê do "1/4"
alguém pode fazer pra mim? obrigada

-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Qua Jun 23, 2010 18:59
por Douglasm » Qua Jun 23, 2010 18:59
Olá Carolzinha. Essa dá um pouco de trabalho, mas vamos lá. Primeiramente façamos o produto AB (eu vou passar batido pelas contas mais básicas, para evitar fazer um post imenso):
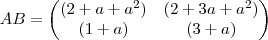
Sabemos que a inversa é igual a:
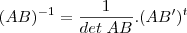
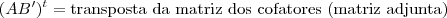
Vamos calcular de uma vez o det AB:
![det AB = (2+a+a^2)\;.\;[(1+a) + 2]\; - \; [(2+a+a^2) + 2a]\;.\;(1+a) = 4+2a+2a^2 - 2a - 2a^2 = 4 det AB = (2+a+a^2)\;.\;[(1+a) + 2]\; - \; [(2+a+a^2) + 2a]\;.\;(1+a) = 4+2a+2a^2 - 2a - 2a^2 = 4](/latexrender/pictures/1956ff42b63d2e9dec41079bf885ec1e.png)
Agora vamos à matriz dos cofatores:
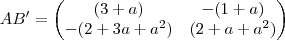
Fazendo a transposta desta, chegamos a adjunta:
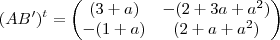
Finalmente chegamos a inversa:
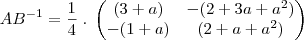
Deste modo, a soma dos elementos da diagonal principal é:
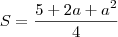
E é isso ai. Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Carolziiinhaaah » Qua Jun 23, 2010 19:42
por Carolziiinhaaah » Qua Jun 23, 2010 19:42
Perfeito *-*
Saquei onde eu estava errando, Douglas
eu estava esquecendo de fazer a transposta da matriz dos cofatores
obrigada, mais uma vez!

-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matriz e diagonal principal
por Drudi_Fer » Dom Jan 19, 2014 16:33
- 1 Respostas
- 2793 Exibições
- Última mensagem por e8group

Seg Fev 03, 2014 20:30
Matrizes e Determinantes
-
- Se A é uma matriz 5x5 cujos elementos fora da diagonal são n
por jlr2906 » Sáb Set 01, 2018 05:01
- 0 Respostas
- 5002 Exibições
- Última mensagem por jlr2906

Sáb Set 01, 2018 05:01
Álgebra Linear
-
- Qual o valor principal
por William Frank » Seg Nov 10, 2014 09:51
- 3 Respostas
- 2040 Exibições
- Última mensagem por William Frank

Qua Nov 12, 2014 22:59
Matemática Financeira
-
- Área e diagonal do paralelogramo/-help
por Trapezius » Qua Mai 31, 2017 01:38
- 0 Respostas
- 3148 Exibições
- Última mensagem por Trapezius

Qua Mai 31, 2017 01:38
Trigonometria
-
- inverso da potência
por aynee » Sex Jul 18, 2014 12:37
- 2 Respostas
- 2093 Exibições
- Última mensagem por aynee

Sex Jul 18, 2014 18:35
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
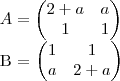
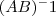 é igual a:
é igual a: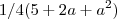

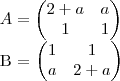
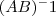 é igual a:
é igual a: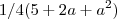

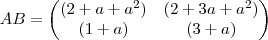
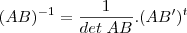
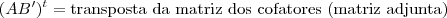
![det AB = (2+a+a^2)\;.\;[(1+a) + 2]\; - \; [(2+a+a^2) + 2a]\;.\;(1+a) = 4+2a+2a^2 - 2a - 2a^2 = 4 det AB = (2+a+a^2)\;.\;[(1+a) + 2]\; - \; [(2+a+a^2) + 2a]\;.\;(1+a) = 4+2a+2a^2 - 2a - 2a^2 = 4](/latexrender/pictures/1956ff42b63d2e9dec41079bf885ec1e.png)
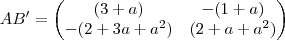
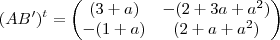
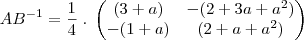
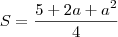



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
