 por hevhoram » Seg Jun 21, 2010 13:26
por hevhoram » Seg Jun 21, 2010 13:26
ola pessoal fiquei em duvida numa questao de um concurso
é o seguinte:
sabemos que o cociente de dois numeros irracionais pode ser um numero racional. Das alternativas abaixo, qual exemplifica essa afirmação?
a) \frac{\sqrt[]{2}}{\sqrt[]{4}} = \frac{1}{\sqrt[]{2}}
b) \frac{\sqrt[]{2}}{\sqrt[]{18}} = \frac{1}{\sqrt[]{9}}
fiz meios por extemos e deu 1 as duas alternativas porque então a resposta é letra b????
porque a letra a nao vai resultar tambem num numero racional???
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por MarceloFantini » Ter Jun 22, 2010 00:53
por MarceloFantini » Ter Jun 22, 2010 00:53
Porque a a letra é o número
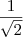
, que é um número irracional. Na letra b, no entanto, dá
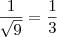
, pois sabemos que
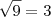
, logo, a fração é racional.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- raiz para numero racional
por hevhoram » Seg Jun 21, 2010 13:19
- 6 Respostas
- 2873 Exibições
- Última mensagem por MarceloFantini

Sáb Jun 26, 2010 11:29
Álgebra Elementar
-
- número:racional
por Victor Gabriel » Seg Jun 17, 2013 16:40
- 0 Respostas
- 1122 Exibições
- Última mensagem por Victor Gabriel

Seg Jun 17, 2013 16:40
Teoria dos Números
-
- Número Racional
por marinalcd » Ter Set 19, 2017 17:13
- 0 Respostas
- 1538 Exibições
- Última mensagem por marinalcd

Ter Set 19, 2017 17:13
Aritmética
-
- [Integral de fração racional] Deduza uma formiula para:
por Job1992 » Ter Nov 26, 2013 22:29
- 1 Respostas
- 1764 Exibições
- Última mensagem por e8group

Sáb Nov 30, 2013 21:27
Cálculo: Limites, Derivadas e Integrais
-
- Função Racional - preciso de ajuda para hoje ainda!
por raf » Seg Set 28, 2015 14:32
- 1 Respostas
- 2611 Exibições
- Última mensagem por nakagumahissao

Sex Out 02, 2015 00:47
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


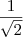 , que é um número irracional. Na letra b, no entanto, dá
, que é um número irracional. Na letra b, no entanto, dá 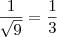 , pois sabemos que
, pois sabemos que 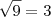 , logo, a fração é racional.
, logo, a fração é racional.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.