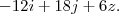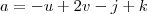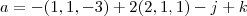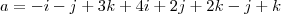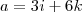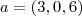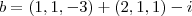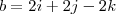por guigo1302 » Sex Jun 18, 2010 22:28
por guigo1302 » Sex Jun 18, 2010 22:28
Boa noite. Tenho o seguinte problema para resolver:
Sejam 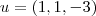 e
e 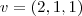 vetores no R³. Verifique se existe um vetor w, de módulo
vetores no R³. Verifique se existe um vetor w, de módulo 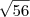 , simultaneamente ortogonal aos vetores
, simultaneamente ortogonal aos vetores 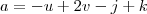 e
e  . (u,v,w,i,j,k são vetores, mas eu não sei faze a setinha em cima).
. (u,v,w,i,j,k são vetores, mas eu não sei faze a setinha em cima).eu achei
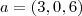
e

também fiz que
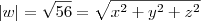
.

Também fiz o produto misto axb para achar um vetor ortogonal. Tive como resultado
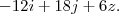
Só que agora eu não sei mais o que fazer. Desculpa se eu postei algo errado, é a primeira vez que utilizo o fórum. E obrigado ;D
-
guigo1302
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Jun 18, 2010 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por DanielFerreira » Seg Jun 21, 2010 13:01
por DanielFerreira » Seg Jun 21, 2010 13:01
Também fiz o produto misto axb para achar um vetor ortogonal. Tive como resultado
achemos o vetor ortogonal através do
produto vetorial.
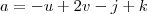
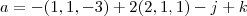
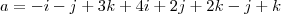
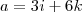
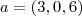

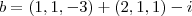

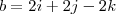
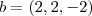
|i j k| i j|
|3 0 6| 3 0|
|2 2 -2| 2 2| =
12j + 6k - 12i + 6j =
- 12i + 18j + 6k =
(- 12, 18, 6)a resposta é não!!!
o módulo é

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
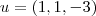 e
e 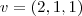 vetores no R³. Verifique se existe um vetor w, de módulo
vetores no R³. Verifique se existe um vetor w, de módulo 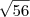 , simultaneamente ortogonal aos vetores
, simultaneamente ortogonal aos vetores 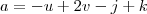 e
e  . (u,v,w,i,j,k são vetores, mas eu não sei faze a setinha em cima).
. (u,v,w,i,j,k são vetores, mas eu não sei faze a setinha em cima).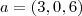 e
e 
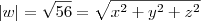 .
.