 por hevhoram » Qua Jun 09, 2010 13:20
por hevhoram » Qua Jun 09, 2010 13:20
19. Três amigos, X, Y e Z, saem para jantar em um
restaurante. Na hora de pagar a conta, que deveria ser
dividida igualmente entre os três, X percebeu que não
tinha dinheiro e Y e Z pagaram a conta, Y contribuindo
com três quintos do total. Mais tarde, X pagou a Y e Z
a quantia de R$ 34,00, o valor que lhe correspondia na
conta. Quanto deste valor caberá a Z?
resposta: R$ 6,80
eu fiz desta forma mas nao deu certo; y +z= 34 , y= 3/5 do total entao z= 2/5 do total então z+ 3/5= 34 z= 33,40 entao 33,40 - 34,00 = 0.60? nao entendi ???
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por MarceloFantini » Qua Jun 09, 2010 21:13
por MarceloFantini » Qua Jun 09, 2010 21:13
Inicialmente, a situação era que

, onde
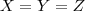
(todos pagam a mesma quantia). Porém, X estava sem dinheiro, então
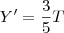
e
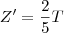
. Vamos analisar a razão do que eles iam pagar e o que eles efetivamente pagaram:

. Isso significa que Y pagou 80% a mais do que o esperado. Analogamente,
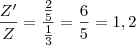
, mostrando que Z pagou 20% a mais do que o esperado. Quando X paga 34 aos dois, isso quer dizer que 80% pertence a Y e 20% pertence a Z, logo:
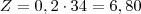
Qualquer dúvida comente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por hevhoram » Qui Jun 10, 2010 13:54
por hevhoram » Qui Jun 10, 2010 13:54
deixa ver se eu entendi , quer dizer que esse 1/3 é por que são 3 pessoas?? se fossem quatro pessoas seria 1/4????
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por MarceloFantini » Qui Jun 10, 2010 14:17
por MarceloFantini » Qui Jun 10, 2010 14:17
Sim. Se você sai com 5 amigos, e vocês vão rachar a conta igualmente, o que vocês fazem? Pegam o valor total e dividem por 6, ou seja, cada um paga

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- regra de tres amigos trabalhando juntos
por hevhoram » Qui Fev 19, 2015 16:43
- 2 Respostas
- 3088 Exibições
- Última mensagem por hevhoram

Seg Fev 23, 2015 10:30
Álgebra Elementar
-
- Amigos do Orkut
por Molina » Qua Jun 10, 2009 11:57
- 1 Respostas
- 1778 Exibições
- Última mensagem por Douglasm

Seg Fev 22, 2010 17:20
Desafios Difíceis
-
- Olá amigos eu calculei certo Urgente
por Catriane Moreira » Seg Nov 08, 2010 20:21
- 1 Respostas
- 1030 Exibições
- Última mensagem por MarceloFantini

Seg Nov 08, 2010 20:33
Matemática Financeira
-
- Amigos não estou conseguindo resolver o exercicio...
por Catriane Moreira » Seg Set 06, 2010 21:56
- 1 Respostas
- 1680 Exibições
- Última mensagem por Cleyson007

Seg Set 06, 2010 23:15
Sistemas de Equações
-
- Amigos me ajudem resolver esse problema
por Catriane Moreira » Sáb Nov 06, 2010 23:11
- 1 Respostas
- 1569 Exibições
- Última mensagem por Rogerio Murcila

Ter Nov 09, 2010 14:35
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , onde
, onde 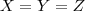 (todos pagam a mesma quantia). Porém, X estava sem dinheiro, então
(todos pagam a mesma quantia). Porém, X estava sem dinheiro, então 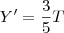 e
e 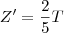 . Vamos analisar a razão do que eles iam pagar e o que eles efetivamente pagaram:
. Vamos analisar a razão do que eles iam pagar e o que eles efetivamente pagaram:  . Isso significa que Y pagou 80% a mais do que o esperado. Analogamente,
. Isso significa que Y pagou 80% a mais do que o esperado. Analogamente, 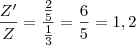 , mostrando que Z pagou 20% a mais do que o esperado. Quando X paga 34 aos dois, isso quer dizer que 80% pertence a Y e 20% pertence a Z, logo:
, mostrando que Z pagou 20% a mais do que o esperado. Quando X paga 34 aos dois, isso quer dizer que 80% pertence a Y e 20% pertence a Z, logo: 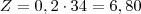


 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

