19. Três amigos, X, Y e Z, saem para jantar em um
restaurante. Na hora de pagar a conta, que deveria ser
dividida igualmente entre os três, X percebeu que não
tinha dinheiro e Y e Z pagaram a conta, Y contribuindo
com três quintos do total. Mais tarde, X pagou a Y e Z
a quantia de R$ 34,00, o valor que lhe correspondia na
conta. Quanto deste valor caberá a Z?
resposta: R$ 6,80
eu fiz desta forma mas nao deu certo; y +z= 34 , y= 3/5 do total entao z= 2/5 do total então z+ 3/5= 34 z= 33,40 entao 33,40 - 34,00 = 0.60? nao entendi ???


 , onde
, onde 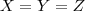 (todos pagam a mesma quantia). Porém, X estava sem dinheiro, então
(todos pagam a mesma quantia). Porém, X estava sem dinheiro, então 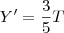 e
e 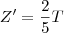 . Vamos analisar a razão do que eles iam pagar e o que eles efetivamente pagaram:
. Vamos analisar a razão do que eles iam pagar e o que eles efetivamente pagaram:  . Isso significa que Y pagou 80% a mais do que o esperado. Analogamente,
. Isso significa que Y pagou 80% a mais do que o esperado. Analogamente, 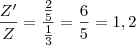 , mostrando que Z pagou 20% a mais do que o esperado. Quando X paga 34 aos dois, isso quer dizer que 80% pertence a Y e 20% pertence a Z, logo:
, mostrando que Z pagou 20% a mais do que o esperado. Quando X paga 34 aos dois, isso quer dizer que 80% pertence a Y e 20% pertence a Z, logo: 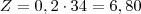


 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)