![Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}} Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/36a66fef206b9437d9cce91685d3689e.png)
![Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}} Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/b6819fc7e51162b592bbcc9210e74346.png)
Por que a razão entre os dispêndios se transforma em:
![\frac{Dx(px,py,r}{Dy(px,py,r}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}} \frac{Dx(px,py,r}{Dy(px,py,r}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}}](/latexrender/pictures/fca2c327245a941f95bbbd6597a991f6.png)
Aí se calcula a derivada dessa razão com o
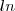 , não entendi porque usar o logarítmo natural na derivada
, não entendi porque usar o logarítmo natural na derivada![\sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)} \sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)}](/latexrender/pictures/89c2c84b2bd9d0feac681d9126bfd88c.png)

![Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}} Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/36a66fef206b9437d9cce91685d3689e.png)
![Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}} Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/b6819fc7e51162b592bbcc9210e74346.png)
![\frac{Dx(px,py,r}{Dy(px,py,r}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}} \frac{Dx(px,py,r}{Dy(px,py,r}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}}](/latexrender/pictures/fca2c327245a941f95bbbd6597a991f6.png)
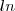 , não entendi porque usar o logarítmo natural na derivada
, não entendi porque usar o logarítmo natural na derivada![\sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)} \sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)}](/latexrender/pictures/89c2c84b2bd9d0feac681d9126bfd88c.png)

jmario escreveu:As funções dipêndios são as seguintes:
Por que a razão entre os dispêndios se transforma em:
A fórmula da elasticidade de substituição é dada por:
Aí se chega nessa equação com apenas a derivada dessa razão com o, não entendi porque usar o logarítmo natural na derivada

jmario escreveu:jmario escreveu:As funções dipêndios são as seguintes:
Por que a razão entre os dispêndios se transforma em:
A fórmula da elasticidade de substituição é dada por:
Aí se chega nessa equação com apenas a derivada dessa razão com o, não entendi porque usar o logarítmo natural na derivada
Alguém pode me ajudar
Grato
José Mario

jmario escreveu:jmario escreveu:As funções dipêndios são as seguintes:
Por que a razão entre os dispêndios se transforma em:
A fórmula da elasticidade de substituição é dada por:
Aí se chega nessa equação com apenas a derivada dessa razão com o, não entendi porque usar o logarítmo natural na derivada
Alguém pode me ajudar
Grato
José Mario
jmario escreveu:jmario escreveu:jmario escreveu:As funções dipêndios são as seguintes:
Por que a razão entre os dispêndios se transforma em:
A fórmula da elasticidade de substituição é dada por:
Aí se chega nessa equação com apenas a derivada dessa razão com o, não entendi porque usar o logarítmo natural na derivada
Alguém pode me ajudar
Grato
José Mario

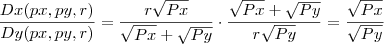 , os
, os  cancelam-se e a mesma coisa com a soma das raízes.
cancelam-se e a mesma coisa com a soma das raízes.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)