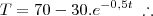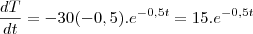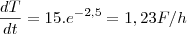por Bruhh » Qua Jun 02, 2010 19:00
por Bruhh » Qua Jun 02, 2010 19:00
Olá, boa tarde
Resolvi alguns exercícios porém, não consigo de forma alguma, resolve-los de forma correta. Alguém poderia me ajudar e ver o que estou fazendo de errado??
-Uma chapa metálica quadrada de lado x está se espandindo segundo a equação x= 2+t², onde a variável t representa o tempo.Determinar a taxa de variação da área desse quadrado no tempo t=2.
Bom pelo o que eu aprendi, eu teria que derivar a função e substituir 2 em t para obter a taxa de variação e como a área é igual ao lado² , ficaria assim:
x= 2+t²
x'=0+2t
x'=2t , com t=2
x'=4cm³/cm
Mas o que acontece é que a minha resposta me informa como resposta 48.Gente de onde eles tiraram esse número??!?-Um copo de limonada a uma temperatura de 40F está em uma sala com temperatura constante de 70F.Pode-se mostrar que se a temperatura da limonada atingir 52F em uma hora, então a temperatura T da limonada como função no tempo decorrido é modelada aproximadamente pela equação T=70-30.
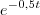
, onde T está em graus F e t em horas.Qual a taxa de variação quando t=5
Bom aqui eu tentei resolver fazendo inicial - final dividido pelo tempo e pela derivação, mas acredito que a forma correta seja a derivação, então fiz assim:
T'=70-30.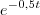 .(-0,5)
.(-0,5)
T'=70-30.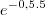 .(-0,5)
.(-0,5)
T'=70-30.0,082084998.(-0,5)
T'=70-30.(-0,041042499)
T'=70+1,231274979
T' -71,23
-71,23A resposta correta é 1,23F/h .Por favor, alguém sabe me dizer o que estou fazendo errado??
Muito Obrigadaa

-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
 por Douglasm » Qua Jun 02, 2010 19:26
por Douglasm » Qua Jun 02, 2010 19:26
Olá Bruhh. Vamos ao primeiro problema:
1) Aqui o enunciado não é totalmente claro em minha opinião. A equação que ele dá é referente a dilatação linear da chapa, por conta disso e do fato da chapa ser quadrada, essa equação deve ser elevada ao quadrado para termos a dilatação superficial:
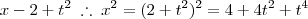
Agora sim derivamos:
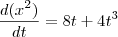
Para t=2:
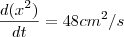
(isso se x estiver em centímetros e o tempo em segundos)
2) Este problema é basicamente igual ao primeiro. Para encontrar a taxa de variação, é só derivar a equação e substituir o valor (já adianto que seu erro foi somente esquecer que a derivada de 70, uma constante, é igual a zero.):
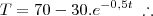
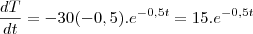
Para t=5:
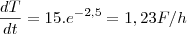
Espero ter ajudado. Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Bruhh » Sáb Jun 05, 2010 18:25
por Bruhh » Sáb Jun 05, 2010 18:25
Muito obrigada, entendi tudo direitinho.
Obrigada


-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicações da Derivada
por Thyago Quimica » Seg Out 29, 2012 18:44
- 1 Respostas
- 2878 Exibições
- Última mensagem por e8group

Seg Out 29, 2012 19:15
Cálculo: Limites, Derivadas e Integrais
-
- Aplicaçoes lineares (derivada)
por Zanatta » Qua Mai 15, 2013 22:59
- 0 Respostas
- 884 Exibições
- Última mensagem por Zanatta

Qua Mai 15, 2013 22:59
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações de Derivada - Problemas de Otimização - Socorro!!
por Josi » Ter Nov 03, 2009 17:30
- 1 Respostas
- 2807 Exibições
- Última mensagem por marciommuniz

Ter Nov 03, 2009 22:30
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações de Derivada - Problemas de Otimização - Socorro!!
por Josi » Ter Nov 03, 2009 17:31
- 1 Respostas
- 4765 Exibições
- Última mensagem por Elcioschin

Qua Nov 04, 2009 08:40
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações de Derivada [Teorema do valor médio]
por xanda2012 » Sáb Jun 16, 2012 16:22
- 2 Respostas
- 2266 Exibições
- Última mensagem por xanda2012

Sáb Jun 16, 2012 17:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
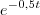 , onde T está em graus F e t em horas.Qual a taxa de variação quando t=5
, onde T está em graus F e t em horas.Qual a taxa de variação quando t=5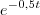 .(-0,5)
.(-0,5)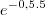 .(-0,5)
.(-0,5) -71,23
-71,23


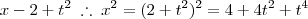
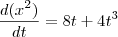
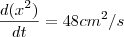 (isso se x estiver em centímetros e o tempo em segundos)
(isso se x estiver em centímetros e o tempo em segundos)