Progressão aritmética aindaaa...

[Alessandrasouza]

Oie gente..entaum.. eu to com uma dúvida de novoo...na verdade é outra pro meesmo assuunto.. É um problema de PA q eu resolvi mas acho q tá muito grande a resolução e nem sei se está de fato correto..É assim:

Alexandre comprou um album com espaço para 660 figurinhas. Td dia ele compra 20 pacotinhos, sendo 5 figurinhas em kd uma. No 1º dia ele colocou todas. No 2º dia, vieram algumas repetidas e colocou 95. No 3º 90 e assim por diante. Calcule o tempo necessáriop/ preencher o album...

E eu fiz assim:

Sn =

660=

660=

660=

660=

2.(660)= 205n-5

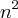
1320= 205n-5

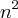
0=-1320+205n-5 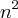dividi td por -5 p/ simplificar

0=264-41n+1 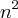virou uma equação de 2ºgrau a=1 b=-41 c=264

resolvendo a equação de 2ºgrau têm-se que n1=33 n2=8

Por isso, eu quero saber se naum tem um jeito de fazer que seja menor....

[MarceloFantini]

O jeito analítico acredito que seja somente esse, mas você pode fazer a soma no braço (não é tão grande).

[Cleyson007]

Boa noite Alessandra e Fantini!

Também não consegui desenvolver outra forma de resolução (acredito que se houver outra forma, não irá fugir muito de P.A...)

O resultado está correto! é interessante observar que a P.A. é decrescente, portanto, .

Achei interessante que a resolução cai numa equação do 2º grau... portanto, duas raízes reais (valores de n).

Fiquei com uma dúvida: "Como se explica o fato de possuírem dos valores que satisfazem (algebricamente) a condição?"

Acredito que a resposta coerente para esse tipo de exercício seja 8 dias.. quando o Alexandre chegar no 33º dia, as figurinhas já não estariam todas coladas?

Até mais.

[MarceloFantini]

Porque eles satisfazem a equação. Lembre-se que a equação não sabe do problema, nós é que sabemos da situação real representada pela equação.