Na figura, as distâncias entre dois pontos horizontais consecutivos e as distâncias entre dois pontos verticais consecutivos são iguais a 1. A região comum ao triângulo e ao quadrado tem área:





Maligno escreveu:Ola
Eu naum vou responder, mas creio que para calcular a area do triangulo basta traçar outros triangulos ao lado, aonde há a linha reta para que possa saber o valor do lado, do quadrado é só multiplicar

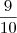


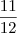
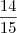

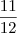 usando geometria analítica. Veja só:
usando geometria analítica. Veja só: 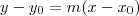 , sendo
, sendo  (reta decrescente e
(reta decrescente e  é o menor ângulo que a reta forma com a horizontal)
é o menor ângulo que a reta forma com a horizontal)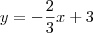
 e
e  (paralelas aos lados direito e superior do quadrado, respectivamente.). Fazendo isso, podemos encontrar as medidas do pequeno triângulo que fica fora do triângulo que contém o quadrado:
(paralelas aos lados direito e superior do quadrado, respectivamente.). Fazendo isso, podemos encontrar as medidas do pequeno triângulo que fica fora do triângulo que contém o quadrado: 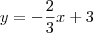 e
e  :
: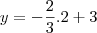
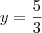
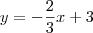 e
e  :
: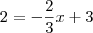
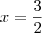
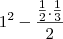 =
= 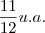

 .
.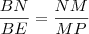
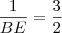
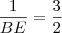
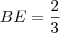

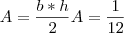
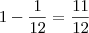



Douglasm escreveu:Olá Molina. Esse seu método é muito mais objetivo. Eu não tinha me tocado que podia afirmar que o lado de cima do triângulo menor era 1/2, assim seria bem mais rápido.
Até a próxima.



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.