 por neilendrigo » Sex Mai 09, 2008 00:18
por neilendrigo » Sex Mai 09, 2008 00:18
Oi... Gostei muito do site de vcs... de grand eutilidade, sou estudando de engenharia elétrica - UDESC.
Bom, preciso tirar umas duvidas urgentes de algebra I, prciso entender até amanhã...
A dúvida é em relação a 2 questões, que são muito parecidads...
1ª
Encontre as equações reduzidas da reta que passa pelos pontos A(1, 4, -3), B(2, 1, 3) e C(4, -1, 7).
desculpa, ia escrever do jeito que resolvi, mas tah errado e tbm não sei colcar vetores nesse programa ai =(, tentei mas não consegui, então lá vai....
encontrei um vetor diretor AB=v, depois peguei v e o ponto c que pertence a reta, e daí através do vetor diretor da reta e e do ponto c, escreve a equaçao parametrica da reta r....
2ª
Encontre as equaçoes reduzidas da reta que passa pelos pontos A(1, 4, 3), B(2, 1, 3) e C(4, -1, 7) e é perpendicular ao eixo x.
a segunda questão, cheguei a desenhá-la, e percebi que a reta ABC é reversa ao eixo x, como consigo contemplar com elas sendo reversas? se elas forem realmente reversas, deveria somente fazer o produto misto e em seguida, caso elas sejam reversas, falar que não é possivel encontrar tais equaçoes pq a reta pedida é reversa ao eixo x??
muito obrigado...
cara, adorei o site de vcs, muiiiito mesmo!
estou na primeira fase de eng. elétrica, e a partir de hoje, utilizarei quase que diariamente a ajuda de vcs, pq realmente preciso, quanto mais estudamos, mais ignorantes percbemos que somos, aff, isso é triste, portanto... como estudarei muiiito... muitas duvidas surgirção, abraços... obrigado pela ajuda!
-
neilendrigo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Mai 08, 2008 23:54
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sex Mai 09, 2008 16:11
por admin » Sex Mai 09, 2008 16:11
Olá neilendrigo, seja bem-vindo!
Agradeço em nome de todos os seus elogios, muito obrigado!
Pensei em seus problemas e eis alguns comentários.
Em primeiro lugar, concordo com o procedimento citado por você para a resolução (1), pois com as equações paramétricas, obtemos então as equações simétricas e por fim as equações reduzidas, isolando as variáveis y e z e expressando-as em função de x.
Mas, o fato é que percebi que os pontos A, B e C não são colineares, nem no primeiro exercício, nem no segundo. Compare com o seu desenho, veja que em cada exercício, a tripla de pontos determina uma face e não uma reta:
Favor confirmar os pontos:
1)

,
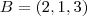
e
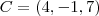
2)
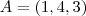
,
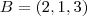
e
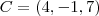
Tanto é que A, B e C seriam colineares se, e somente se, existisse

real, tal que:

Sendo no exercício (1)
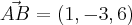
e

:

Não existe lambda que satisfaça as três equações:
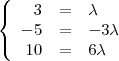
Ou seja, o par ordenado
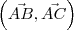
é linearmente independente (LI, portanto, não são paralelos a uma mesma reta).
Analogamente para o exercício 2, mudando o ponto A.
Então, até que estes pontos sejam confirmados, não existe uma única reta que passa por eles (A, B e C ou A', B, C).
Sobre vetores no LaTeX, há alguma sintaxe relacionada, mas acho que a utilização não fica prática para este caso. Melhor utilizar algum outro programa para a "plotagem" e anexar a imagem gerada, caso queira.
Vamos conversando...
Até mais.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por neilendrigo » Sex Mai 09, 2008 23:21
por neilendrigo » Sex Mai 09, 2008 23:21
Nossa, muito obrigado fabio... Quero saber se poderia meio que diariamente escrever duvidas no seu site, pq realmente preciso... na minha universidade o negócio é meio que no vire-se... eu tbm percebi que não eram colineares, mas só a poucas horas atrás, quando tentei refazer, e olha... deu vontade de chorar, pq se bater com algo tão básico por não perceber isso, dá desânimo. Muito obrigado, espero poder crescer com a tua ajuda, e a dos demais membros do site e é claro, fazê-los crescerem tbm =)...
-
neilendrigo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Mai 08, 2008 23:54
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sáb Mai 10, 2008 13:15
por admin » Sáb Mai 10, 2008 13:15
Olá neilendrigo!
Um dos objetivos do site é justamente receber estas dúvidas, desde que acompanhadas das tentativas e dificuldades comentadas, não somente os enunciados de problemas, para que haja uma interação e compreensão, não apenas resolução.
Todas as ajudas são apoiadas por um estudo complementar do assunto, especialmente no caso do ensino superior, onde devo me posicionar como aluno.
Suas mensagens serão bem-vindas, embora o foco esteja nas dúvidas até o ensino médio, em conseqüência da minha formação e porque atual e infelizmente, eu ainda sou o único colaborador ativo nas ajudas.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por neilendrigo » Sáb Mai 10, 2008 15:07
por neilendrigo » Sáb Mai 10, 2008 15:07
Fabio, vou apresentar teu site para meus professores... Penso que vc deveria fazer o mesmo, e todos os demais, simplesmente apresenta-lo, descobri ele do nada, pq estava procurando resoluções na internet e livros... se vc fizer mais propaganda, tenho certeza que muiiiitos colaboradores aparecerão, abraços... ótimo fim de semana =)...
-
neilendrigo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Mai 08, 2008 23:54
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Algebra linear e geometria analítica
por clari_27 » Sáb Mai 12, 2012 17:32
- 1 Respostas
- 1908 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 10:56
Geometria Analítica
-
- Geometria Analitica e Algebra linear
por Danizinhalacerda13 » Qui Mai 01, 2014 19:15
- 1 Respostas
- 2902 Exibições
- Última mensagem por Danizinhalacerda13

Qui Mai 01, 2014 19:25
Geometria Analítica
-
- Algebra linear e geometria analitica. Me ajudem!!!
por clari_27 » Sáb Mai 12, 2012 17:19
- 1 Respostas
- 1838 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 10:48
Geometria Analítica
-
- [Algebra linear e geometria analitica] Duvida
por lucasdemirand » Sáb Jul 06, 2013 15:32
- 1 Respostas
- 1403 Exibições
- Última mensagem por e8group

Dom Jul 07, 2013 21:27
Álgebra Linear
-
- Geometria Analitica e Algebra linear-O plano - Ajuda
por Danizinhalacerda13 » Qui Mai 01, 2014 20:37
- 3 Respostas
- 2422 Exibições
- Última mensagem por Cleyson007

Sáb Mai 03, 2014 10:15
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ,
, 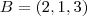 e
e 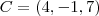
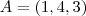 ,
,  real, tal que:
real, tal que:
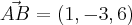 e
e  :
:
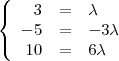
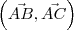 é linearmente independente (LI, portanto, não são paralelos a uma mesma reta).
é linearmente independente (LI, portanto, não são paralelos a uma mesma reta).


 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
