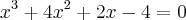 ?
?

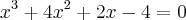 ?
?
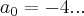
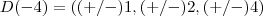 ,aqui ja responde a pergunta.discorremos mais.
,aqui ja responde a pergunta.discorremos mais.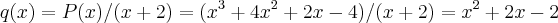
![x=-1+\sqrt[]{3}...x=-1-\sqrt[]{3} x=-1+\sqrt[]{3}...x=-1-\sqrt[]{3}](/latexrender/pictures/ea6efd897563100ac06dad145f99e945.png) que sao raizes irracionais.assim como as raizes complexas sao em pares,assim tambem sao as raizes irracionais.logo se dado um polinomio e encontramos uma raiz do tipo
que sao raizes irracionais.assim como as raizes complexas sao em pares,assim tambem sao as raizes irracionais.logo se dado um polinomio e encontramos uma raiz do tipo![x=a+b\sqrt[]{c}...a,b,c \in Z,c\neq 0 x=a+b\sqrt[]{c}...a,b,c \in Z,c\neq 0](/latexrender/pictures/db592e87526de3f1cdd885fc877bb2bf.png) teremos tambem
teremos tambem![x=a-b\sqrt[]{c}... x=a-b\sqrt[]{c}...](/latexrender/pictures/143580062d41d06f06e6a0d28ed8c9f6.png)
![\sqrt[]{2},-\sqrt[]{2}...\sqrt[]{p},-\sqrt[]{p},p(primo)...
1+q\sqrt[]{p}...etc... \sqrt[]{2},-\sqrt[]{2}...\sqrt[]{p},-\sqrt[]{p},p(primo)...
1+q\sqrt[]{p}...etc...](/latexrender/pictures/f3a9d81614782481eff0d60d8a814927.png)

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



