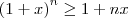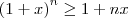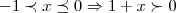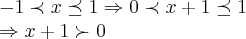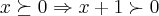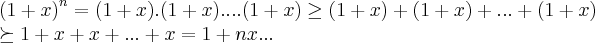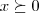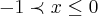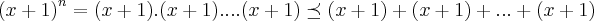por adauto martins » Sex Abr 23, 2021 15:35
por adauto martins » Sex Abr 23, 2021 15:35
(ITA-1959)mostrar se é verdadeiro
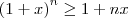
onde n é um inteiro positivo e x é qualquer numero maior ou igual a 1.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Abr 23, 2021 15:55
por adauto martins » Sex Abr 23, 2021 15:55
soluçao
essa desiqualdade é conhecida como "desiqualdade de bernoulli".usa-se em maior parte a induçao finita para demonstra-la,mas aqui usarei uma simples algebra para se ter o resultado.
p/
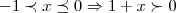
de fato
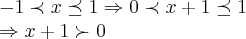
p/
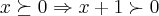
logo
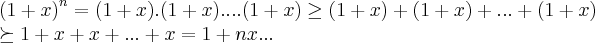
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Dom Abr 25, 2021 12:50
por adauto martins » Dom Abr 25, 2021 12:50
correçao
a demonstraçao acima vale para
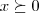
no intervalo
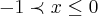
teriamos
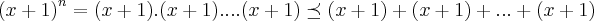
o qual invalidaria a forma da demonstraçao...
quando eu tiver uma forma demonstravel dessa desiqualdade(que esta correta,e demonstravel via induçao finita)
eu a postarei...obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercicio resolvido
por adauto martins » Sex Jul 15, 2016 14:48
- 0 Respostas
- 33703 Exibições
- Última mensagem por adauto martins

Sex Jul 15, 2016 14:48
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Qua Jul 20, 2016 18:35
- 0 Respostas
- 31787 Exibições
- Última mensagem por adauto martins

Qua Jul 20, 2016 18:35
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Ter Jul 26, 2016 17:43
- 0 Respostas
- 22017 Exibições
- Última mensagem por adauto martins

Ter Jul 26, 2016 17:43
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Sáb Ago 13, 2016 11:28
- 0 Respostas
- 17069 Exibições
- Última mensagem por adauto martins

Sáb Ago 13, 2016 11:28
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Sex Out 18, 2019 14:29
- 2 Respostas
- 22855 Exibições
- Última mensagem por adauto martins

Sex Out 18, 2019 15:42
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.