 por adauto martins » Seg Out 28, 2019 16:02
por adauto martins » Seg Out 28, 2019 16:02
(escola militar do realengo,rj-exame de admissao 1934)
estudar a variaçao e traçar o grafico de:
![y=x+\sqrt[]{(x-1)/(x+1)} y=x+\sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/0b72509d662227a539b6655d74484715.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Out 28, 2019 16:36
por adauto martins » Seg Out 28, 2019 16:36
soluçao:
aqui vou me resumir ao calculo de maximos e minimos(variaçao da funçao).para traçar o grafico deve-se achar as raizes de y,
localizar os pontos criticos(maximos,minimos,inflexao e etc...)
o dominio da funçao e´para
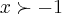
,ponto importante,que como em exercicios anteriores,nao o fiz...deve-se sempre...
entao para calcularmos os maximos,ou minimos,devemos:
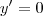
entao
![y=x+\sqrt[]{(x-1)/(x+1)}
y'=x'+(\sqrt[]{(x-1)/(x+1)})' y=x+\sqrt[]{(x-1)/(x+1)}
y'=x'+(\sqrt[]{(x-1)/(x+1)})'](/latexrender/pictures/db92906ef0d34004b41a7354c649f30f.png)
aqui usaremos a derivada do quociente e a regra da cadeia,pois
![\sqrt[]{(x-1)/(x+1)} \sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/1788ab9e3ffc96c54152fd86cecba059.png)
é composta,logo:
![y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))'(*) y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))'(*)](/latexrender/pictures/06fcade0e95ca08f9ea396204da09f50.png)
vamos calcular separadamente a funçao
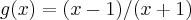
e depois recoloca-la em (*),entao
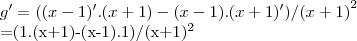
voltando em(*)
![y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))' y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))'](/latexrender/pictures/bd66a0e9253a6f5c5fc6a70b36628f1e.png)
![y'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))/{(x+1)}^{2}=0 y'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))/{(x+1)}^{2}=0](/latexrender/pictures/67327ae6eb92ec69bc98bb66cb93e91c.png)

![(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
\sqrt[]{(x-1)/(x+1)}=-2{(x+1)}^{2}/((x+1)-(x-1)) (\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
\sqrt[]{(x-1)/(x+1)}=-2{(x+1)}^{2}/((x+1)-(x-1))](/latexrender/pictures/eeb4157e548d933ea4474b84ad5e9f49.png)
uma equaçao racional ...
![(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
{(x-1)/(x+1)={(-2{(x+1)}^{2}/((x+1)-(x-1))}^{2}... (\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
{(x-1)/(x+1)={(-2{(x+1)}^{2}/((x+1)-(x-1))}^{2}...](/latexrender/pictures/a678733e38b2b4e76f5829a1bac77af7.png)
para "facilitar" os calculo,podemos fazer:
y=(x+1)...z=(x-1)...
termine-o aos interessados,pois eu cansei...
mas é isso...depois calcular a derivada segunda e testar os pontos de maximos(
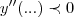
) e os minimos (
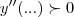
)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Out 28, 2019 17:32
por adauto martins » Seg Out 28, 2019 17:32
derivei erroneamente a funçao y:
podemos faz.
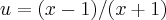
e...depois refaço esse exercicio...no mais,obrigado...
ps-se alguem se habilitar,faça-o...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Out 28, 2019 21:52
por adauto martins » Seg Out 28, 2019 21:52
vamos voltar ao exercicio e resolver corretamente,assim espero...
vamos derivar a funçao
![u=\sqrt[]{(x-1)/(x+1)} u=\sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/0a054ab3a6385476079c497759c98893.png)
vamos fazer z=(x+1) e w=x-1
![u=\sqrt[]{w/z} u=\sqrt[]{w/z}](/latexrender/pictures/73049bc694e38ae229d92a5826df3124.png)
entao:
![u'=(1/2)(w/z)'.(\sqrt[]{z/w})
u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2} u'=(1/2)(w/z)'.(\sqrt[]{z/w})
u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2}](/latexrender/pictures/708afb9c9a24072486c354ecde30802c.png)
pois w'=z'=1...
![u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}{2} u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}{2}](/latexrender/pictures/f2baf88c221b4a0d3f765c8e610ef167.png)
logo
![y'=1+ (1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2}(*) y'=1+ (1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2}(*)](/latexrender/pictures/2811e640deace6267a4fe0c1d72c766a.png)
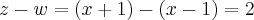
![\Rightarrow 1+(\sqrt[]{z/w})/{(z)}^{2}=0
\sqrt[]{z/w}=-{z}^{2}
z/w={z}^{4}\Rightarrow {z}^{3}w=1 \Rightarrow 1+(\sqrt[]{z/w})/{(z)}^{2}=0
\sqrt[]{z/w}=-{z}^{2}
z/w={z}^{4}\Rightarrow {z}^{3}w=1](/latexrender/pictures/63ddb485800943e8d357421c088cd1ab.png)
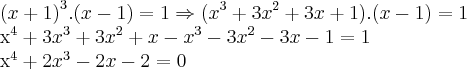
bom,temos agora um polinomio de quarto grau para solucionar...
1) o raio de localizaçao das raizes é dado por:
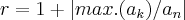
onde
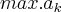
é o maior dos coeficientes do pólinomio e
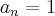
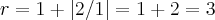
ou seja,as raizes estao no intervalo [-3,3]
sabemos que o dominio da funçao é
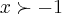
,logo
o intervalo sera (-1,3].
bom,o restante fica como exercicio...
possiveis raizes racionais (-1/2,1/2,1,2)...
ps-adiante faremos um estudo mais detalhado de raizes de polinomios...obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![y=x+\sqrt[]{(x-1)/(x+1)} y=x+\sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/0b72509d662227a539b6655d74484715.png)

![y=x+\sqrt[]{(x-1)/(x+1)} y=x+\sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/0b72509d662227a539b6655d74484715.png)

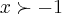 ,ponto importante,que como em exercicios anteriores,nao o fiz...deve-se sempre...
,ponto importante,que como em exercicios anteriores,nao o fiz...deve-se sempre...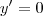
![y=x+\sqrt[]{(x-1)/(x+1)}
y'=x'+(\sqrt[]{(x-1)/(x+1)})' y=x+\sqrt[]{(x-1)/(x+1)}
y'=x'+(\sqrt[]{(x-1)/(x+1)})'](/latexrender/pictures/db92906ef0d34004b41a7354c649f30f.png)
![\sqrt[]{(x-1)/(x+1)} \sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/1788ab9e3ffc96c54152fd86cecba059.png)
![y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))'(*) y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))'(*)](/latexrender/pictures/06fcade0e95ca08f9ea396204da09f50.png)
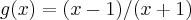
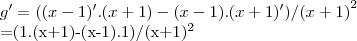
![y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))' y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))'](/latexrender/pictures/bd66a0e9253a6f5c5fc6a70b36628f1e.png)
![y'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))/{(x+1)}^{2}=0 y'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))/{(x+1)}^{2}=0](/latexrender/pictures/67327ae6eb92ec69bc98bb66cb93e91c.png)

![(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
\sqrt[]{(x-1)/(x+1)}=-2{(x+1)}^{2}/((x+1)-(x-1)) (\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
\sqrt[]{(x-1)/(x+1)}=-2{(x+1)}^{2}/((x+1)-(x-1))](/latexrender/pictures/eeb4157e548d933ea4474b84ad5e9f49.png)
![(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
{(x-1)/(x+1)={(-2{(x+1)}^{2}/((x+1)-(x-1))}^{2}... (\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
{(x-1)/(x+1)={(-2{(x+1)}^{2}/((x+1)-(x-1))}^{2}...](/latexrender/pictures/a678733e38b2b4e76f5829a1bac77af7.png)
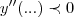 ) e os minimos (
) e os minimos (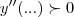 )
)
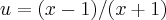 e...depois refaço esse exercicio...no mais,obrigado...
e...depois refaço esse exercicio...no mais,obrigado...
![u=\sqrt[]{(x-1)/(x+1)} u=\sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/0a054ab3a6385476079c497759c98893.png)
![u=\sqrt[]{w/z} u=\sqrt[]{w/z}](/latexrender/pictures/73049bc694e38ae229d92a5826df3124.png)
![u'=(1/2)(w/z)'.(\sqrt[]{z/w})
u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2} u'=(1/2)(w/z)'.(\sqrt[]{z/w})
u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2}](/latexrender/pictures/708afb9c9a24072486c354ecde30802c.png)
![u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}{2} u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}{2}](/latexrender/pictures/f2baf88c221b4a0d3f765c8e610ef167.png)
![y'=1+ (1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2}(*) y'=1+ (1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2}(*)](/latexrender/pictures/2811e640deace6267a4fe0c1d72c766a.png)
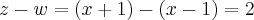
![\Rightarrow 1+(\sqrt[]{z/w})/{(z)}^{2}=0
\sqrt[]{z/w}=-{z}^{2}
z/w={z}^{4}\Rightarrow {z}^{3}w=1 \Rightarrow 1+(\sqrt[]{z/w})/{(z)}^{2}=0
\sqrt[]{z/w}=-{z}^{2}
z/w={z}^{4}\Rightarrow {z}^{3}w=1](/latexrender/pictures/63ddb485800943e8d357421c088cd1ab.png)
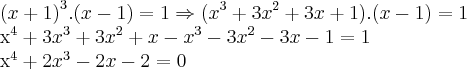
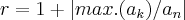
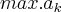 é o maior dos coeficientes do pólinomio e
é o maior dos coeficientes do pólinomio e 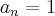
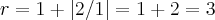
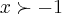 ,logo
,logo





