estudar a variaçao e traçar o grafico de:
![y=x+\sqrt[]{(x-1)/(x+1)} y=x+\sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/0b72509d662227a539b6655d74484715.png)

![y=x+\sqrt[]{(x-1)/(x+1)} y=x+\sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/0b72509d662227a539b6655d74484715.png)

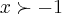 ,ponto importante,que como em exercicios anteriores,nao o fiz...deve-se sempre...
,ponto importante,que como em exercicios anteriores,nao o fiz...deve-se sempre...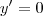
![y=x+\sqrt[]{(x-1)/(x+1)}
y'=x'+(\sqrt[]{(x-1)/(x+1)})' y=x+\sqrt[]{(x-1)/(x+1)}
y'=x'+(\sqrt[]{(x-1)/(x+1)})'](/latexrender/pictures/db92906ef0d34004b41a7354c649f30f.png)
![\sqrt[]{(x-1)/(x+1)} \sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/1788ab9e3ffc96c54152fd86cecba059.png)
![y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))'(*) y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))'(*)](/latexrender/pictures/06fcade0e95ca08f9ea396204da09f50.png)
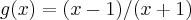
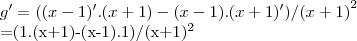
![y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))' y'=1+(\sqrt[]{(x-1)/(x+1)})'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x-1)/(x+1))'](/latexrender/pictures/bd66a0e9253a6f5c5fc6a70b36628f1e.png)
![y'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))/{(x+1)}^{2}=0 y'=1+(1/2)(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))/{(x+1)}^{2}=0](/latexrender/pictures/67327ae6eb92ec69bc98bb66cb93e91c.png)

![(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
\sqrt[]{(x-1)/(x+1)}=-2{(x+1)}^{2}/((x+1)-(x-1)) (\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
\sqrt[]{(x-1)/(x+1)}=-2{(x+1)}^{2}/((x+1)-(x-1))](/latexrender/pictures/eeb4157e548d933ea4474b84ad5e9f49.png)
![(\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
{(x-1)/(x+1)={(-2{(x+1)}^{2}/((x+1)-(x-1))}^{2}... (\sqrt[]{(x-1)/(x+1)}).((x+1)-(x-1))=-2{(x+1)}^{2}
{(x-1)/(x+1)={(-2{(x+1)}^{2}/((x+1)-(x-1))}^{2}...](/latexrender/pictures/a678733e38b2b4e76f5829a1bac77af7.png)
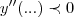 ) e os minimos (
) e os minimos (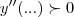 )
)
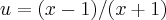 e...depois refaço esse exercicio...no mais,obrigado...
e...depois refaço esse exercicio...no mais,obrigado...
![u=\sqrt[]{(x-1)/(x+1)} u=\sqrt[]{(x-1)/(x+1)}](/latexrender/pictures/0a054ab3a6385476079c497759c98893.png)
![u=\sqrt[]{w/z} u=\sqrt[]{w/z}](/latexrender/pictures/73049bc694e38ae229d92a5826df3124.png)
![u'=(1/2)(w/z)'.(\sqrt[]{z/w})
u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2} u'=(1/2)(w/z)'.(\sqrt[]{z/w})
u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2}](/latexrender/pictures/708afb9c9a24072486c354ecde30802c.png)
![u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}{2} u'=(1/2)(\sqrt[]{z/w})(z-w)/{(z)}{2}](/latexrender/pictures/f2baf88c221b4a0d3f765c8e610ef167.png)
![y'=1+ (1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2}(*) y'=1+ (1/2)(\sqrt[]{z/w})(z-w)/{(z)}^{2}(*)](/latexrender/pictures/2811e640deace6267a4fe0c1d72c766a.png)
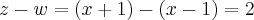
![\Rightarrow 1+(\sqrt[]{z/w})/{(z)}^{2}=0
\sqrt[]{z/w}=-{z}^{2}
z/w={z}^{4}\Rightarrow {z}^{3}w=1 \Rightarrow 1+(\sqrt[]{z/w})/{(z)}^{2}=0
\sqrt[]{z/w}=-{z}^{2}
z/w={z}^{4}\Rightarrow {z}^{3}w=1](/latexrender/pictures/63ddb485800943e8d357421c088cd1ab.png)
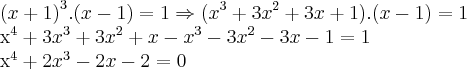
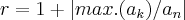
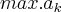 é o maior dos coeficientes do pólinomio e
é o maior dos coeficientes do pólinomio e 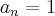
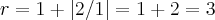
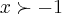 ,logo
,logo
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

