 por adauto martins » Sáb Out 26, 2019 19:46
por adauto martins » Sáb Out 26, 2019 19:46
(ENE-escola nacional de engenharia da universidade do brasil,rj-exame de ad.1958)
calcule a area compreendida entre as curvas

e
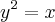
.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Out 26, 2019 20:09
por adauto martins » Sáb Out 26, 2019 20:09
soluçao:
primeiramente temos que ter

,pois

.
vamos achar os pontos onde essas curvas se interceptam...temos:
![y=\sqrt[]{x}...y={x}^{2}
\sqrt[]{x}={x}^{2} y=\sqrt[]{x}...y={x}^{2}
\sqrt[]{x}={x}^{2}](/latexrender/pictures/d161882409fd4925b3674ca336690339.png)
![{x}^{4}-x=0\Rightarrow x({x}^{3}-1)=0
x=0...x=\sqrt[]{1}=1...x,y\in \Re {x}^{4}-x=0\Rightarrow x({x}^{3}-1)=0
x=0...x=\sqrt[]{1}=1...x,y\in \Re](/latexrender/pictures/a09f3c5c92301949adf52f316da71147.png)
para calcular a area pedida,que é dada por:
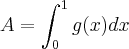
onde
![g(x)=\sqrt[]{x}-{x}^{2} g(x)=\sqrt[]{x}-{x}^{2}](/latexrender/pictures/046c6983fa3c90d96f9642e5b7008483.png)
, pois
![\sqrt[]{x}\geq {x}^{2} \sqrt[]{x}\geq {x}^{2}](/latexrender/pictures/f9146ddfddad8f5e265edeb9838fe6e6.png)
...(pq?)
logo:
![A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx=\int_{0}^{1}(\sqrt[]{x})dx-\int_{0}^{1}{x}^{2}dx=
A=(1/(1/2)+1){x}^{(1/2+1)}[0,1]-(1/(2+1)){x}^{1+2}[0,1]=
=(2/3){x}^{3/2}[0,1]-(1/3){x}^{3}[0,1]=...=(2/3)-(1/3)=1/3 A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx=\int_{0}^{1}(\sqrt[]{x})dx-\int_{0}^{1}{x}^{2}dx=
A=(1/(1/2)+1){x}^{(1/2+1)}[0,1]-(1/(2+1)){x}^{1+2}[0,1]=
=(2/3){x}^{3/2}[0,1]-(1/3){x}^{3}[0,1]=...=(2/3)-(1/3)=1/3](/latexrender/pictures/03f7353edea5c10f8d145d4c2792572f.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e 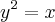 .
.
 e
e 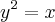 .
.
 ,pois
,pois  .
.![y=\sqrt[]{x}...y={x}^{2}
\sqrt[]{x}={x}^{2} y=\sqrt[]{x}...y={x}^{2}
\sqrt[]{x}={x}^{2}](/latexrender/pictures/d161882409fd4925b3674ca336690339.png)
![{x}^{4}-x=0\Rightarrow x({x}^{3}-1)=0
x=0...x=\sqrt[]{1}=1...x,y\in \Re {x}^{4}-x=0\Rightarrow x({x}^{3}-1)=0
x=0...x=\sqrt[]{1}=1...x,y\in \Re](/latexrender/pictures/a09f3c5c92301949adf52f316da71147.png)
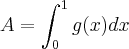
![g(x)=\sqrt[]{x}-{x}^{2} g(x)=\sqrt[]{x}-{x}^{2}](/latexrender/pictures/046c6983fa3c90d96f9642e5b7008483.png) , pois
, pois ![\sqrt[]{x}\geq {x}^{2} \sqrt[]{x}\geq {x}^{2}](/latexrender/pictures/f9146ddfddad8f5e265edeb9838fe6e6.png) ...(pq?)
...(pq?)![A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx=\int_{0}^{1}(\sqrt[]{x})dx-\int_{0}^{1}{x}^{2}dx=
A=(1/(1/2)+1){x}^{(1/2+1)}[0,1]-(1/(2+1)){x}^{1+2}[0,1]=
=(2/3){x}^{3/2}[0,1]-(1/3){x}^{3}[0,1]=...=(2/3)-(1/3)=1/3 A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx=\int_{0}^{1}(\sqrt[]{x})dx-\int_{0}^{1}{x}^{2}dx=
A=(1/(1/2)+1){x}^{(1/2+1)}[0,1]-(1/(2+1)){x}^{1+2}[0,1]=
=(2/3){x}^{3/2}[0,1]-(1/3){x}^{3}[0,1]=...=(2/3)-(1/3)=1/3](/latexrender/pictures/03f7353edea5c10f8d145d4c2792572f.png)



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.