(UDF-universidade do distrito federal,rj-exame 1947)
calcular o volume de uma esfera,cujo circulo maximo é o circulo circunscrito a um triangulo equilatero de 4m de lado.
ps-A UDF-rj é a atual UERJ.
por adauto martins » Ter Out 22, 2019 11:26
por adauto martins » Ter Out 22, 2019 12:01
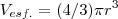
![tg 30=r/2\Rightarrow r=2.tg 30=2(sen 30/cos30)
r=2(\sqrt[]{3}/2 /(1/2)=2.\sqrt[]{3}](/latexrender/pictures/d85476451c9f37d08eac7db0da160db3.png "tg 30=r/2\Rightarrow r=2.tg 30=2(sen 30/cos30)
r=2(\sqrt[]{3}/2 /(1/2)=2.\sqrt[]{3}")
![{V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3} )}^{3}=(8/3)3\sqrt[]{3}\pi
V=8.\pi.\sqrt[]{3}...](/latexrender/pictures/2e8b28afc2645cf05b98ab34b643682f.png "{V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3} )}^{3}=(8/3)3\sqrt[]{3}\pi
V=8.\pi.\sqrt[]{3}...")
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)![{V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3})}^{3}=(4/3).\pi({2})^{3}\sqrt[]{3}.\sqrt[]{3}.\sqrt[]{3}=(4/3).8.\pi.3.\sqrt[]{3}=24\pi\sqrt[]{3}...](/latexrender/pictures/1d856d08a79a250de8bf09ca8c02371b.png "{V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3})}^{3}=(4/3).\pi({2})^{3}\sqrt[]{3}.\sqrt[]{3}.\sqrt[]{3}=(4/3).8.\pi.3.\sqrt[]{3}=24\pi\sqrt[]{3}...")