 por adauto martins » Ter Out 22, 2019 11:26
por adauto martins » Ter Out 22, 2019 11:26
(UDF-universidade do distrito federal,rj-exame 1947)
calcular o volume de uma esfera,cujo circulo maximo é o circulo circunscrito a um triangulo equilatero de 4m de lado.
ps-A UDF-rj é a atual UERJ.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Ter Out 22, 2019 12:01
por adauto martins » Ter Out 22, 2019 12:01
soluçao
o volume de uma esfera é dado por
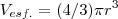
logo temos que encontrar o raio do circulo circunscrito ao triangulo,que no caso o circulo esta dentro do triangul(circulo circunscrito)
![tg 30=r/2\Rightarrow r=2.tg 30=2(sen 30/cos30)
r=2(\sqrt[]{3}/2 /(1/2)=2.\sqrt[]{3} tg 30=r/2\Rightarrow r=2.tg 30=2(sen 30/cos30)
r=2(\sqrt[]{3}/2 /(1/2)=2.\sqrt[]{3}](/latexrender/pictures/d85476451c9f37d08eac7db0da160db3.png)
pois o triangulo é equilatero,e o triangulo para obtençao do raio do circulo sera um triangulo retangulo isosceles de angulo 30°,tendo como catetos r e 2,metade do lado do triangulo maior,onde o circulo esta inscrito.logo
![{V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3} )}^{3}=(8/3)3\sqrt[]{3}\pi
V=8.\pi.\sqrt[]{3}... {V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3} )}^{3}=(8/3)3\sqrt[]{3}\pi
V=8.\pi.\sqrt[]{3}...](/latexrender/pictures/2e8b28afc2645cf05b98ab34b643682f.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Ter Out 22, 2019 13:04
por adauto martins » Ter Out 22, 2019 13:04
uma correçao:
![{V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3})}^{3}=(4/3).\pi({2})^{3}\sqrt[]{3}.\sqrt[]{3}.\sqrt[]{3}=(4/3).8.\pi.3.\sqrt[]{3}=24\pi\sqrt[]{3}... {V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3})}^{3}=(4/3).\pi({2})^{3}\sqrt[]{3}.\sqrt[]{3}.\sqrt[]{3}=(4/3).8.\pi.3.\sqrt[]{3}=24\pi\sqrt[]{3}...](/latexrender/pictures/1d856d08a79a250de8bf09ca8c02371b.png)
obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



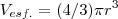
![tg 30=r/2\Rightarrow r=2.tg 30=2(sen 30/cos30)
r=2(\sqrt[]{3}/2 /(1/2)=2.\sqrt[]{3} tg 30=r/2\Rightarrow r=2.tg 30=2(sen 30/cos30)
r=2(\sqrt[]{3}/2 /(1/2)=2.\sqrt[]{3}](/latexrender/pictures/d85476451c9f37d08eac7db0da160db3.png)
![{V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3} )}^{3}=(8/3)3\sqrt[]{3}\pi
V=8.\pi.\sqrt[]{3}... {V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3} )}^{3}=(8/3)3\sqrt[]{3}\pi
V=8.\pi.\sqrt[]{3}...](/latexrender/pictures/2e8b28afc2645cf05b98ab34b643682f.png)

![{V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3})}^{3}=(4/3).\pi({2})^{3}\sqrt[]{3}.\sqrt[]{3}.\sqrt[]{3}=(4/3).8.\pi.3.\sqrt[]{3}=24\pi\sqrt[]{3}... {V}_{esf.}=(4/3)\pi{(2.\sqrt[]{3})}^{3}=(4/3).\pi({2})^{3}\sqrt[]{3}.\sqrt[]{3}.\sqrt[]{3}=(4/3).8.\pi.3.\sqrt[]{3}=24\pi\sqrt[]{3}...](/latexrender/pictures/1d856d08a79a250de8bf09ca8c02371b.png)


 .
.



