![A=\sqrt[]{{2}^{20}+{2}^{23}}](/latexrender/pictures/9f474edb4a42633632aa67728e45ed51.png "A=\sqrt[]{{2}^{20}+{2}^{23}}")
Preciso diminuir a expressão,
Tentei da seguinte forma:
![\sqrt[]{{2}^{20}}+\sqrt[]{{2}^{23}}
1024+\sqrt[]{{2}^{20}* {2}^{3}}
1024+1024* \sqrt[]{{2}^{3}}
2048* \sqrt[]{{2}^{3}}](/latexrender/pictures/1b124b9eff4db59fa1c027297e38e581.png "\sqrt[]{{2}^{20}}+\sqrt[]{{2}^{23}}
1024+\sqrt[]{{2}^{20}* {2}^{3}}
1024+1024* \sqrt[]{{2}^{3}}
2048* \sqrt[]{{2}^{3}}")
O gabarito da questão diz que a resposta é:
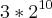
Como chego nesse resultado? mas quero saber as propriedades aplicadas para aprender como faz
Obrigado galera...
por mrclsaraiva » Sex Abr 28, 2017 23:42
por mrclsaraiva » Qui Mai 04, 2017 09:55
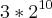
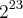se transforma em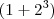 
por petras » Ter Ago 01, 2017 12:56
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)![\\A^2=2^{20}+2^23\rightarrow A^2=2^{20}(1+2^3)\rightarrow A^2=2^{20}.9\rightarrow\\\
\\\
A=\sqrt{2^{20}.9}\rightarrow \boxed{A =2^{10}.3}](/latexrender/pictures/55a774d8efef20d00b9dcbb2e912a4bb.png "\\A^2=2^{20}+2^23\rightarrow A^2=2^{20}(1+2^3)\rightarrow A^2=2^{20}.9\rightarrow\\\
\\\
A=\sqrt{2^{20}.9}\rightarrow \boxed{A =2^{10}.3}")