Dividindo-se o polinômio p(x) = x3 + kx2 + 6x + 2 por q(x) = x2 – 2x, obtém-se o resto r(x) = 3x + 2. O valor de k é: a) 7/2 b) 2/7 c) -2/3 d) -3/2 e) -7/2
Eu já tentei fazer esse cálculo de todas as formas mas não consigo encontrar nenhuma das respostas . Preciso de ajuda para identificar o cálculo que preciso fazer


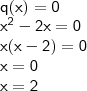
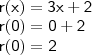
 por
por 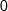 em
em 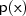 , então deverá encontrar
, então deverá encontrar 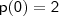 . Verifique!!
. Verifique!!
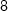 em
em 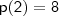 .
.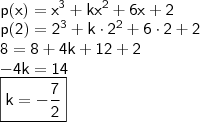


 .
.
 :
: