 por adauto martins » Qua Jul 27, 2016 18:45
por adauto martins » Qua Jul 27, 2016 18:45
seja
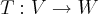
uma transformaçao linear,onde
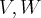
sao espaços vetoriais sobre um corpo
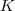
,mostre que:
a)
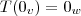
...
b)se
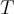
injetiva e
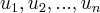
de
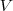
sao

,entao
{

}é uma base de

...
soluçao:
a)
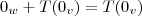
,condiçao de existencia do elemento neutro da

,logo:
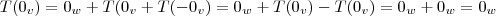
...
b)
seja
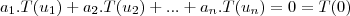
,como
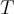
é linear,teremos:
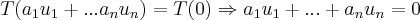
,como
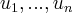
sao
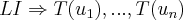
sao

e portanto uma base de

...cqd...
ps-se T for sobrejetiva,entao V=W(fica como exercicio)...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Jul 28, 2016 11:02
por adauto martins » Qui Jul 28, 2016 11:02
refazendo parte esquecida da letra b)...
como temos q.
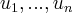
sao
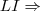
a unica soluçao p/...

sera
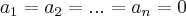
,logo
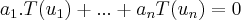
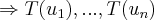
sao

e portanto uma base de
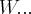
...obrigado...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [P.A.] Exercício
por Cleyson007 » Dom Mai 25, 2008 13:02
- 1 Respostas
- 6563 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 13:20
Progressões
-
- Exercício de PA
por Cleyson007 » Dom Jun 01, 2008 02:45
- 1 Respostas
- 11349 Exibições
- Última mensagem por admin

Dom Jun 01, 2008 14:31
Progressões
-
- Exercício de PA e PG
por Cleyson007 » Sáb Jun 14, 2008 01:21
- 3 Respostas
- 15309 Exibições
- Última mensagem por DanielFerreira

Sex Jul 24, 2009 11:59
Progressões
-
- exercicio de P.G.
por Gir » Qui Jul 02, 2009 18:21
- 3 Respostas
- 4428 Exibições
- Última mensagem por Gir

Sex Jul 03, 2009 10:12
Progressões
-
- exercicio de P.G.
por Gir » Seg Jul 06, 2009 10:54
- 1 Respostas
- 3376 Exibições
- Última mensagem por Marcampucio

Seg Jul 06, 2009 16:33
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
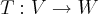 uma transformaçao linear,onde
uma transformaçao linear,onde 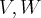 sao espaços vetoriais sobre um corpo
sao espaços vetoriais sobre um corpo 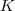 ,mostre que:
,mostre que: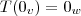 ...
...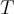 injetiva e
injetiva e 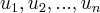 de
de 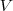 sao
sao  ,entao
,entao  }é uma base de
}é uma base de  ...
...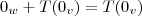 ,condiçao de existencia do elemento neutro da
,condiçao de existencia do elemento neutro da  ,logo:
,logo: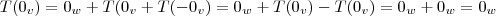 ...
...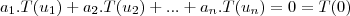 ,como
,como 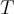 é linear,teremos:
é linear,teremos: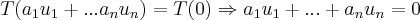 ,como
,como 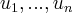 sao
sao 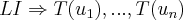 sao
sao  e portanto uma base de
e portanto uma base de  ...cqd...
...cqd...

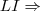 a unica soluçao p/...
a unica soluçao p/... sera
sera 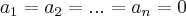 ,logo
,logo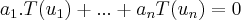
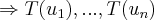
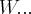 ...obrigado...
...obrigado...
 .
.
 :
: