A questão parece ter sido colocada de forma diferente. De qualquer forma para agilizar e não ter que resolver a questao novamente:
https://br.answers.yahoo.com/question/i ... 000AA6JkTJpossui a soma ateh 360 sem repetir o 4.
Portanto, a resposta do link acima estah correta pois 1/3 do tempo os números ficam próximos de 1 enquanto que os outros 1/3 dos valores se situam proximos de 0.5 e outros 1/3 proximos de 0. Assim, de 0 graus ateh 90, temos uma PA de razao 2 onde o primeiro termo eh 0 e o ultimo termo eh 90, ou seja
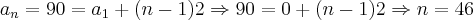
Sao 46 termos. O que equivale a dizer que 46/3 = 15 aproximadamente ficam em torno de 1 e outros 15 em torno de 1/2, ou seja, 15 + 15/2 = 23 aproximadamente
Se repetirmos isso para os quatro quadrantes, e considerando que os cossenos estão elevados ao quadrado, ou seja, sempre positivos, temos então que multiplicar esse valor por 4, ou seja, 23 x 4 = 92 aproximadamente.
Fiz um aplicativo para verificar isso em valores e mostra-los para voce e os resultados sao:

Se desejar baixar o aplicativo:
https://drive.google.com/file/d/0B05xwwRHqMfYelNBaXpacFR0TDA/view?usp=sharingAgora, no seu caso, basta adicionar ao resultado mais um Cos^2(4), o que daria 92 + 0.9951340344 =92.99513403
Nao mudaria muito o resultado. Basta agora escolher a opcao cujo valor seja mais proximo de 92.99513403
Veja que o valor final correto da soma seria: 90.6024899481915 + cos^2(4) = 91.59762398
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali


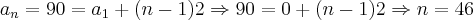

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.