´Senhores o enunciado é o seguinte: Duas partículas realizam movimentos descritos pelas equações das retas r1 = t(1, 2) e r2 = (1, 0) + t(?1, ?1), t ? R. Pode haver colisão das partículas em algum instante?
Essa resolução está um pouco vaga veja:
Basta ver se têm a mesma posição no mesmo instante de tempo.
(t, 2t)=(1-t, -t) se somente se t=1-t e 2t=-t se somente se t=1/2 e t=0.
Concluímos pois que as duas particulas nunca ocupam a mesma posição no mesmo instante de tempo, não haverá colisão.


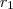 sai da origem e segue linearmente com
sai da origem e segue linearmente com 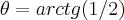 ...
...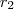 parte do eixo das abicissas e declina em
parte do eixo das abicissas e declina em 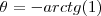 ...
...
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)