 por Lipe » Seg Fev 29, 2016 20:49
por Lipe » Seg Fev 29, 2016 20:49
´Senhores o enunciado é o seguinte: Duas partículas realizam movimentos descritos pelas equações das retas r1 = t(1, 2) e r2 = (1, 0) + t(?1, ?1), t ? R. Pode haver colisão das partículas em algum instante?
Essa resolução está um pouco vaga veja:
Basta ver se têm a mesma posição no mesmo instante de tempo.
(t, 2t)=(1-t, -t) se somente se t=1-t e 2t=-t se somente se t=1/2 e t=0.
Concluímos pois que as duas particulas nunca ocupam a mesma posição no mesmo instante de tempo, não haverá colisão.
-
Lipe
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 29, 2016 20:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Lipe » Sáb Mar 05, 2016 19:42
por Lipe » Sáb Mar 05, 2016 19:42
Tá difícil???
-
Lipe
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 29, 2016 20:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Dom Mar 06, 2016 12:35
por adauto martins » Dom Mar 06, 2016 12:35
nao havera colisao(cruzamento dos graficos)...
o grafico de
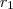
sai da origem e segue linearmente com
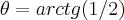
...
o grafico de
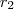
parte do eixo das abicissas e declina em
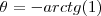
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3157 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- [Equações] Determinar Frações de equações
por fenixxx » Ter Fev 28, 2012 21:28
- 2 Respostas
- 4156 Exibições
- Última mensagem por fenixxx

Qua Fev 29, 2012 17:08
Funções
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3436 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equações
por Neperiano » Qua Fev 11, 2009 12:33
- 6 Respostas
- 6501 Exibições
- Última mensagem por marcio silva

Sex Mar 20, 2009 20:15
Sistemas de Equações
-
- Equações
por Luna » Qui Set 10, 2009 19:30
- 2 Respostas
- 2274 Exibições
- Última mensagem por Luna

Sex Set 11, 2009 19:54
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


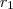 sai da origem e segue linearmente com
sai da origem e segue linearmente com 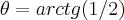 ...
...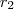 parte do eixo das abicissas e declina em
parte do eixo das abicissas e declina em 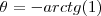 ...
...
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
