Olá gente! Tentei de todas as formas montar uma equação para o problema abaixo, mas não conseguir de jeito nenhum. Por favor, me ajudem a saber como interpretar e como montar a equação.
Um grupo de 50 pessoas fez um orçamento inicial para organizar uma festa, que seria dividido entre elas em cotas iguais.
Verificou-se ao final, que para arcar com todas as despesas, faltavam R$ 510,00, e 5 novas pessoas haviam ingressado no grupo.
No acerto foi decidido que a despesa total seria dividida em partes iguais pelas 55 pessoas. Quem não havia contribuído pagaria a sua parte, e
cada uma das 50 pessoas do grupo inicial deveria contribuir com mais R$ 7,00.
De acordo com essas informações, qual foi o valor da cota calculada no acerto final para cada uma das 55 pessoas?
o valor previsto a ser pago pelas 50 pessoas, então podemos concluir que a quantia a ser paga por cada uma delas é dada por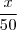 
.
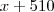, portanto, cada uma dessas pessoas deverá arcar com 
.
.
.
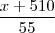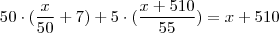