 por thb » Qua Jul 01, 2015 12:58
por thb » Qua Jul 01, 2015 12:58
Em uma cidade com 126.000 habitantes, na qual apenas 1/3 é de homens, sabe-se que 45% da população têm mais de 50 anos de idade.
Nessas condições, o número de mulheres dessa cidade, acima de 50 anos, é igual a:
Não tenho o gabarito dessa questão, mas as opções são estas:
01) 35140
02) 35270
03) 35450
04) 35720
05) 35910
Eu peguei 45% da população total (população acima de 50 anos) e retirei 2/3, que seriam as mulheres. O resultado (2/3 de 45%) não é o certo.
-
thb
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jul 01, 2015 12:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Medicina
- Andamento: cursando
 por Baltuilhe » Qua Jul 01, 2015 16:59
por Baltuilhe » Qua Jul 01, 2015 16:59
Boa tarde!
Tentei fazer a questão da forma como você fez (o seu raciocínio está correto) e não cheguei a nenhum resultado conforme a questão.
Procurei na internet e achei a questão nesta prova (
http://www.consultec.com.br/provas/UNIPE_2014_2_cad1_A.pdf) conforme abaixo:
Vacina contra herpes-zóster
Ela chega ao país para evitar a reativação de um vírus presente em 95% da
população.
A farmacêutica americana MSD acaba de lançar no Brasil um imunizante que
previne o herpes-zóster, causado pelo vírus varicela-zóster. Num primeiro
momento (geralmente na infância), esse agente infeccioso provoca catapora.
Porém, mesmo com o problema curado, ele permanece no corpo em estado
de latência por décadas. Quando o sistema imune está vulnerável, volta a
atacar — daí vem o zóster. “Surgem lesões dolorosas na pele, principalmente
na região das costelas”, diz a médica Rosana Richtmann, da Sociedade
Brasileira de Infectologia. A vacina, indicada a quem tem mais de 50 anos,
visa justamente impedir esse quadro. (BIERNATH, 2014, p. 18).
Questão 36:
Em uma cidade do nordeste brasileiro com 126.000 habitantes, na qual apenas 1/3 é
de homens, sabe-se que 45% da população têm mais de 50 anos de idade.
Nessas condições, de acordo com o texto, o número de mulheres dessa cidade, em idade
indicada para tomar a vacina contra herpes-zóster, com chance de ter o vírus presente
em seu organismo, é igual a
01) 35140 03) 35450 05) 35910
02) 35270 04) 35720
Fazendo as contas igual fez chegamos em:
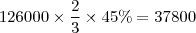
Mas, conforme o início do texto,
...Ela chega ao país para evitar a reativação de um vírus presente em 95% da
população...
, então:
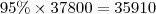
(5)
Espero ter ajudado!

-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Conjunto vazio está dentro de outro conjunto vazio?
por JDomingos » Dom Jul 20, 2014 07:41
- 1 Respostas
- 2231 Exibições
- Última mensagem por DanielFerreira

Dom Jul 20, 2014 12:14
Conjuntos
-
- Conjunto
por Douglaspimentel » Qui Mar 18, 2010 16:52
- 4 Respostas
- 4329 Exibições
- Última mensagem por MarceloFantini

Qua Mai 12, 2010 13:49
Álgebra Elementar
-
- Conjunto
por aline2010 » Dom Jun 13, 2010 22:56
- 1 Respostas
- 1898 Exibições
- Última mensagem por Molina

Seg Jun 14, 2010 00:27
Álgebra Elementar
-
- CONJUNTO
por Douglaspimentel » Sex Dez 10, 2010 16:35
- 0 Respostas
- 1694 Exibições
- Última mensagem por Douglaspimentel

Sex Dez 10, 2010 16:35
Álgebra Elementar
-
- CONJUNTO
por Douglaspimentel » Sex Dez 10, 2010 16:37
- 0 Respostas
- 1423 Exibições
- Última mensagem por Douglaspimentel

Sex Dez 10, 2010 16:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


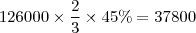
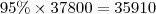 (5)
(5)

