 por jeremiashenrique » Ter Abr 21, 2015 12:16
por jeremiashenrique » Ter Abr 21, 2015 12:16
Pessoal, novamente estou aqui pedindo ajuda sobre esse conteúdo. Pensei que tinha entendido alguma coisa, mas olhando essas questões mais enroladas percebi que não entendi nada. Eu faço Administração, mas praticamente estamos sem professor, pois ele não esta recebendo o pagamento dele, minha turma inteira esta com dificuldades nisso. Eu peço que se por gentileza vcs responderem a questão, façam uma gentileza maior ainda que é comentar, me ensinar. Obrigado!
- Anexos
-

- limites de funções
-
jeremiashenrique
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Abr 17, 2015 15:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração de empresas
- Andamento: cursando
 por adauto martins » Qua Abr 22, 2015 20:43
por adauto martins » Qua Abr 22, 2015 20:43
1)
vou fazer a primeira,as outras sao semelhantes...
p/valores maiores ou igual a 2,diz q. o limite p/ x indo ao ponto 2,sera:
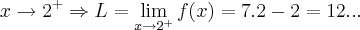
p/valores menores q. 2,
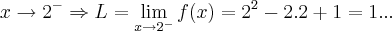
como os limites laterais no ponto 2 sao diferentes, entao nao existe
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por jeremiashenrique » Qui Abr 23, 2015 00:18
por jeremiashenrique » Qui Abr 23, 2015 00:18
valeu
-
jeremiashenrique
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Abr 17, 2015 15:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração de empresas
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4793 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4444 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
-
- Limite de funções
 por jeremiashenrique » Sex Abr 17, 2015 16:07
por jeremiashenrique » Sex Abr 17, 2015 16:07
- 1 Respostas
- 1625 Exibições
- Última mensagem por DanielFerreira

Sex Abr 17, 2015 20:32
Funções
-
- Limite de funções
 por jeremiashenrique » Sex Abr 17, 2015 16:07
por jeremiashenrique » Sex Abr 17, 2015 16:07
- 1 Respostas
- 1642 Exibições
- Última mensagem por adauto martins

Seg Abr 20, 2015 20:57
Funções
-
- [Limite] Funções trigonométricas
por Aliocha Karamazov » Qui Out 27, 2011 18:13
- 4 Respostas
- 2042 Exibições
- Última mensagem por Aliocha Karamazov

Sex Out 28, 2011 03:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



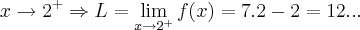
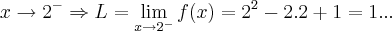
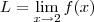 ...
...






