 por lucasnb » Seg Fev 23, 2015 13:38
por lucasnb » Seg Fev 23, 2015 13:38
Fala galera, gostaria de uma ajuda pra resolver esta questão. Já tentei umas par de vez e nada, poderiam me dar uma luz? Ficarei grato.
Numa obra de saneamento básico, 30 operários levaram 49 dias para escavar uma vala de 400 m de comprimento, 1,5 m de profundidade e 60 cm de largura. Se o número de operários é diminuído em 30%, a profundidade diminuída em 20% e a largura aumentada em 50%, então, o número de dias necessários para escavar uma vala de 200 m, será igual a:
a) 42
b) 49
c) 28
d) 35
e) 56
Gabarito fala que é A.
Poderiam me ajudar?
-
lucasnb
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 23, 2015 13:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Baltuilhe » Qua Fev 25, 2015 13:13
por Baltuilhe » Qua Fev 25, 2015 13:13
Bom dia!
Vamos montar um quadro as variáveis:
Operários diminuem em 30%; 30 x 30% = 9; 30-9 = 21
Profundidade diminui em 20%; 1,5 x 20% = 0,3; 1,5-0,3 = 1,2
Largura aumenta em 50%; 60 x 50% = 30; 60+30 = 90

Agora verificamos quais variáveis são diretamente proporcionais e quais inversamente proporcionais com relação ao tempo, teremos:
Tempo x Operários = Inversamente Proporcionais (Menos operários, mais tempo)
Tempo x Comprimento / Profundidade / Largura = Diretamente Proporcionais
Montando a equação:
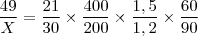
Simplificando:


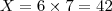
Espero ter ajudado!
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
 por lucasnb » Qua Fev 25, 2015 16:31
por lucasnb » Qua Fev 25, 2015 16:31
Muito Obrigado pela resposta Baltuilhe, só estou com mais uma dúvida.
No caso do comprimento e profundidade por que elas são diretamente proporcionais ao tempo? Se diminui operários, leva mais tempo. Se aumenta o tempo, e diminui o comprimento e profundidade não teria que ser grandezas inversamente proporcionais, pois precisa de menos tempo já que a quantidade de metros vai ser menor?
Já no caso da largura, se aumenta o tempo e aumenta a largura, elas são diretamente proporcionais.
-
lucasnb
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 23, 2015 13:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Baltuilhe » Qua Fev 25, 2015 18:55
por Baltuilhe » Qua Fev 25, 2015 18:55
Boa tarde!
Para montar a regra de 3 composta deve ter em mente que as comparações para serem descobertas se são diretamente ou inversamente proporcionais devem ser somente da variável que se calcula e com cada uma das outras envolvidas.
No caso, como queríamos calcular o tempo tínhamos que comparar:
Tempo com Operários = Inversamente proporcional
Tempo com Comprimento = Diretamente proporcional
Tempo com Profundidade = Diretamente proporcional
Tempo com Largura = Diretamente proporcional.
Não se compara a profundidade com a quantidade de operários pois ambas as variáveis já estão completas, não são elas que devem ser calculadas.
Espero ter ajudado!
Abraços!
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- regra de tres composta
por Liliani » Qui Mar 18, 2010 16:35
- 2 Respostas
- 5616 Exibições
- Última mensagem por Liliani

Qua Mar 31, 2010 17:23
Pedidos
-
- Regra de três composta
por Danilo Dias Vilela » Qua Ago 25, 2010 11:44
- 0 Respostas
- 1902 Exibições
- Última mensagem por Danilo Dias Vilela

Qua Ago 25, 2010 11:44
Álgebra Elementar
-
- regra de três composta
por hevhoram » Dom Mai 22, 2011 22:07
- 1 Respostas
- 2564 Exibições
- Última mensagem por Molina

Seg Mai 23, 2011 00:59
Álgebra Elementar
-
- regra de tres composta
por alissonade » Sex Ago 03, 2012 14:01
- 2 Respostas
- 2573 Exibições
- Última mensagem por alissonade

Sáb Ago 04, 2012 00:52
Álgebra Elementar
-
- Regra de três composta
por oescolhido » Ter Fev 12, 2013 21:01
- 1 Respostas
- 2133 Exibições
- Última mensagem por young_jedi

Dom Fev 17, 2013 10:45
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



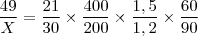


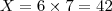

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
